
”¾ĢāÄæ”æŌĶĮĻĀĮŠ²ÄĮĻ£¬¹ŲÓŚxµÄ·½³Ģ£ŗx+![]() £½c+
£½c+![]() µÄ½āŹĒx1£½c£¬x2£½
µÄ½āŹĒx1£½c£¬x2£½![]() £»x©
£»x©![]() £½c©
£½c©![]() µÄ½āŹĒx1£½c£¬x2£½©
µÄ½āŹĒx1£½c£¬x2£½©![]() £»x+
£»x+![]() £½c+
£½c+![]() µÄ½āŹĒx1£½c£¬x2£½
µÄ½āŹĒx1£½c£¬x2£½![]() £»x+
£»x+![]() £½c+
£½c+![]() µÄ½āŹĒx1£½c£¬x2£½
µÄ½āŹĒx1£½c£¬x2£½![]() £»””
£»””
£Ø1£©Ēė¹Ū²ģÉĻŹö·½³ĢÓė½āµÄĢŲÕ÷£¬±Č½Ļ¹ŲÓŚxµÄ·½³Ģx+![]() £½c+
£½c+![]() £Øa”Ł0£©ÓėĖüĆĒµÄ¹ŲĻµ²ĀĻėĖüµÄ½āŹĒŹ²Ć“£¬²¢ĄūÓĆ”°·½³ĢµÄ½ā”±µÄøÅÄī½ųŠŠŃéÖ¤£®
£Øa”Ł0£©ÓėĖüĆĒµÄ¹ŲĻµ²ĀĻėĖüµÄ½āŹĒŹ²Ć“£¬²¢ĄūÓĆ”°·½³ĢµÄ½ā”±µÄøÅÄī½ųŠŠŃéÖ¤£®
£Ø2£©æÉŅŌÖ±½ÓĄūÓĆ£Ø1£©µÄ½įĀŪ£¬½ā¹ŲÓŚxµÄ·½³Ģ£ŗx+![]() £½a+
£½a+![]() £®
£®
”¾“š°ø”æ£Ø1£©·½³ĢµÄ½āĪŖx1£½c£¬x2£½![]() ,ŃéÖ¤¼ū½āĪö£»£Ø2£©x£½aÓėx£½
,ŃéÖ¤¼ū½āĪö£»£Ø2£©x£½aÓėx£½![]() ¶¼ĪŖ·ÖŹ½·½³ĢµÄ½ā£®
¶¼ĪŖ·ÖŹ½·½³ĢµÄ½ā£®
”¾½āĪö”æ
£Ø1£©øł¾Ż²ÄĮĻ¼“æÉÅŠ¶Ļ·½³ĢµÄ½ā£¬Č»ŗó“śČėµ½·½³ĢµÄ×óÓŅĮ½±ß¼ģŃ鼓æÉ£»
£Ø2£©½«·½³Ģ×óÓŅĮ½±ßĶ¬Ź±¼õČ„3£¬±äĪŖĢāøÉÖŠµÄŠĪŹ½£¬¼“æÉµĆ³ö“š°ø.
£Ø1£©·½³ĢµÄ½āĪŖx1£½c£¬x2£½![]() £¬
£¬
ŃéÖ¤£ŗµ±x£½cŹ±£¬
”ß×ó±ß£½c+![]() £¬ÓŅ±ß£½c+
£¬ÓŅ±ß£½c+![]() £¬
£¬
”ą×ó±ß£½ÓŅ±ß£¬
”ąx£½cŹĒx+![]() £½c+
£½c+![]() µÄ½ā£¬
µÄ½ā£¬
Ķ¬ĄķæÉµĆ£ŗx£½![]() ŹĒx+
ŹĒx+![]() £½c+
£½c+![]() µÄ½ā£»
µÄ½ā£»
£Ø2£©·½³ĢÕūĄķµĆ£ŗ£Øx©3£©+![]() £½£Øa©3£©+
£½£Øa©3£©+![]() £¬
£¬
½āµĆ£ŗx©3£½a©3»ņx©3£½![]() £¬¼“x£½a»ņx£½
£¬¼“x£½a»ņx£½![]() £¬
£¬
¾¼ģŃéx£½aÓėx£½![]() ¶¼ĪŖ·ÖŹ½·½³ĢµÄ½ā£®
¶¼ĪŖ·ÖŹ½·½³ĢµÄ½ā£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĆęŹĒŠ”Ć÷Éč¼ĘµÄ”°×÷Čż½ĒŠĪµÄøßĻß”±µÄ³ß¹ę×÷Ķ¼¹ż³Ģ.

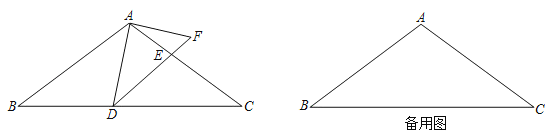
ŅŃÖŖ£ŗ”÷ABC£®
Ēó×÷£ŗBC±ßÉĻµÄøßĻߣ®
×÷·Ø£ŗČēĶ¼£¬
¢Ł·Ö±šŅŌA£¬BĪŖŌ²ŠÄ£¬“óÓŚ![]() ³¤ĪŖ°ė¾¶»»”£¬Į½»”½»ÓŚµćD£¬E£»
³¤ĪŖ°ė¾¶»»”£¬Į½»”½»ÓŚµćD£¬E£»
¢Ś×÷Ö±ĻßDE£¬ÓėAB½»ÓŚµćF£¬ŅŌµćFĪŖŌ²ŠÄ£¬FA³¤ĪŖ°ė¾¶»Ō²£¬½»CBµÄŃÓ³¤ĻßÓŚµćG£»
¢ŪĮ¬½ÓAG£®
ĖłŅŌĻ߶ĪAG¾ĶŹĒĖłĒó×÷µÄBC±ßÉĻµÄøßĻߣ®

øł¾ŻŠ”Ć÷Éč¼ĘµÄ³ß¹ę×÷Ķ¼¹ż³Ģ£¬
£Ø1£©Ź¹ÓĆÖ±³ßŗĶŌ²¹ę£¬²¹Č«Ķ¼ŠĪ£»£Ø±£Įō×÷Ķ¼ŗŪ¼££©
£Ø2£©Ķź³ÉĻĀĆęÖ¤Ć÷.
Ö¤Ć÷£ŗĮ¬½ÓDA£¬DB£¬EA£¬EB£¬
”ßDA=DB£¬
”ąµćDŌŚĻ߶ĪABµÄ“¹Ö±Ę½·ÖĻßÉĻ£Ø £©£ØĢīĶĘĄķµÄŅĄ¾Ż£©£®
”ß = £¬
”ąµćEŌŚĻ߶ĪABµÄ“¹Ö±Ę½·ÖĻßÉĻ£®
”ąDEŹĒĻ߶ĪABµÄ“¹Ö±Ę½·ÖĻߣ®
”ąFA=FB£®
”ąABŹĒ”ŃFµÄÖ±¾¶£®
”ą”ĻAGB=90”ć£Ø £©£ØĢīĶĘĄķµÄŅĄ¾Ż£©£®
”ąAG”ĶBC
¼“AG¾ĶŹĒBC±ßÉĻµÄøßĻߣ®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æѧŠ£“ņĖćÓĆ³¤![]() Ć׵ĥ鰏Ī§³ĒŅ»øö³¤·½ŠĪµÄÉśĪļŌ°ĖĒŃųŠ”ĶĆ£¬ÉśĪļŌ°µÄŅ»ĆęææŌŚ³¤ĪŖ
Ć׵ĥ鰏Ī§³ĒŅ»øö³¤·½ŠĪµÄÉśĪļŌ°ĖĒŃųŠ”ĶĆ£¬ÉśĪļŌ°µÄŅ»ĆęææŌŚ³¤ĪŖ![]() Ć×µÄĒ½ÉĻ£ØČēĶ¼£©£®
Ć×µÄĒ½ÉĻ£ØČēĶ¼£©£®

£Ø1£©ČōÉśĪļŌ°µÄĆ껿ĪŖ![]() Ę½·½Ć×£¬ĒóÉśĪļŌ°µÄ³¤ŗĶæķ£»
Ę½·½Ć×£¬ĒóÉśĪļŌ°µÄ³¤ŗĶæķ£»
£Ø2£©ÄÜ·ńĪ§³ĒĆ껿ĪŖ![]() Ę½·½Ć×µÄÉśĪļŌ°£æČōÄÜ£¬Ēó³ö³¤ŗĶæķ£»Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£®
Ę½·½Ć×µÄÉśĪļŌ°£æČōÄÜ£¬Ēó³ö³¤ŗĶæķ£»Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖĢŻŠĪABCOµÄµ×±ßAOŌŚ![]() ÖįÉĻ£¬
ÖįÉĻ£¬![]() £¬AB”ĶAO£¬¹żµćCµÄĖ«ĒśĻß
£¬AB”ĶAO£¬¹żµćCµÄĖ«ĒśĻß![]() ½»OBÓŚD£¬ĒŅ
½»OBÓŚD£¬ĒŅ![]() £¬Čō”÷OBCµÄĆ껿µČÓŚ3£¬ŌņkµÄÖµĪŖ__________£®
£¬Čō”÷OBCµÄĆ껿µČÓŚ3£¬ŌņkµÄÖµĪŖ__________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬±ß³¤ĪŖ3Õż·½ŠĪ![]() µÄ¶„µć
µÄ¶„µć![]() ÓėŌµćÖŲŗĻ£¬µć
ÓėŌµćÖŲŗĻ£¬µć![]() ŌŚ
ŌŚ![]() Öį£¬
Öį£¬![]() ÖįÉĻ”£·“±ČĄżŗÆŹż
ÖįÉĻ”£·“±ČĄżŗÆŹż![]() µÄĶ¼Ļó½»
µÄĶ¼Ļó½»![]() ÓŚµć
ÓŚµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬
£¬![]() .
.
£Ø1£©Ē󷓱ȥżŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©¹żµć![]() ×÷
×÷![]() ÖįµÄĘ½ŠŠĻß
ÖįµÄĘ½ŠŠĻß![]() £¬µć
£¬µć![]() ŌŚÖ±Ļß
ŌŚÖ±Ļß![]() ÉĻŌĖ¶Æ£¬µć
ÉĻŌĖ¶Æ£¬µć![]() ŌŚ
ŌŚ![]() ÖįÉĻŌĖ¶Æ.
ÖįÉĻŌĖ¶Æ.
¢ŁČō![]() ŹĒŅŌ
ŹĒŅŌ![]() ĪŖÖ±½Ē¶„µćµÄµČŃüÖ±½ĒČż½ĒŠĪ£¬Ēó
ĪŖÖ±½Ē¶„µćµÄµČŃüÖ±½ĒČż½ĒŠĪ£¬Ēó![]() µÄĆ껿£»
µÄĆ껿£»
¢Ś½«”°¢Ł”±ÖŠµÄ”°ŅŌ![]() ĪŖÖ±½Ē¶„µćµÄ”±Č„µō£¬½«ĪŹĢāøÄĪŖ”°Čō
ĪŖÖ±½Ē¶„µćµÄ”±Č„µō£¬½«ĪŹĢāøÄĪŖ”°Čō![]() ŹĒµČŃüÖ±½ĒČż½ĒŠĪ”±£¬
ŹĒµČŃüÖ±½ĒČż½ĒŠĪ”±£¬![]() µÄĆ껿³żĮĖ”°¢Ł”±ÖŠĒóµĆµÄ½į¹ūĶā£¬»¹æÉŅŌŹĒ______.£ØÖ±½ÓŠ““š°ø£¬²»ÓĆŠ“²½Öč£©
µÄĆ껿³żĮĖ”°¢Ł”±ÖŠĒóµĆµÄ½į¹ūĶā£¬»¹æÉŅŌŹĒ______.£ØÖ±½ÓŠ““š°ø£¬²»ÓĆŠ“²½Öč£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
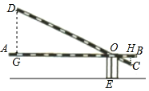
”¾ĢāÄæ”æČēĶ¼£¬Ä³Š”ĒųĆÅæŚµÄĄøøĖ“ÓĖ®Ę½Ī»ÖĆABČĘ¹Ģ¶ØµćOŠż×Ŗµ½Ī»ÖĆDC£¬ŅŃÖŖĄøøĖABµÄ³¤ĪŖ3.5Ć×£¬OAµÄ³¤ĪŖ3Ć×£¬µćCµ½ABµÄ¾ąĄėĪŖ0.3Ć×£¬Ö§ÖłOEµÄøßĪŖ0.6Ć×£¬ÄĒĆ“ĄøøĖ¶ĖµćDĄėµŲĆęµÄ¾ąĄėĪŖ____________Ć×
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB£½AC£½10£¬BC£½16£¬µćDĪŖBC±ßÉĻµÄŅ»øö¶Æµć£ØµćD²»ÓėµćB”¢µćCÖŲŗĻ£©£®ŅŌDĪŖ¶„µć×÷”ĻADE£½”ĻB£¬ÉäĻßDE½»AC±ßÓŚµćE£¬¹żµćA×÷AF”ĶAD½»ÉäĻßDEÓŚµćF£®
£Ø1£©ĒóÖ¤£ŗABCE£½BDCD£»
£Ø2£©µ±DFĘ½·Ö”ĻADCŹ±£¬ĒóAEµÄ³¤£»
£Ø3£©µ±”÷AEFŹĒµČŃüČż½ĒŠĪŹ±£¬ĒóBDµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
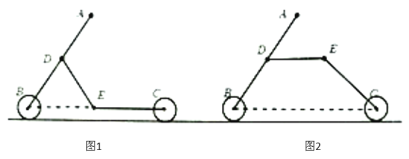
”¾ĢāÄæ”æij¹¤³§Éś²śÄ³ÖÖ¶ą¹¦ÄܶłĶƳµ£¬øł¾ŻŠčŅŖæɱäŠĪĪŖĶ¼1µÄ»¬°å³µ»ņĶ¼2µÄ×ŌŠŠ³µ£¬ŅŃÖŖĒ°ŗó³µĀÖ°ė¾¶ĻąĶ¬£¬![]() £¬
£¬![]() £¬³µøĖ
£¬³µøĖ![]() Óė
Óė![]() Ėł³ÉµÄ
Ėł³ÉµÄ![]() £¬Ķ¼1ÖŠ
£¬Ķ¼1ÖŠ![]() ”¢
Ӣ![]() Ӣ
”¢![]() Čżµć¹²Ļߣ¬Ķ¼2ÖŠµÄ׳°å
Čżµć¹²Ļߣ¬Ķ¼2ÖŠµÄ׳°å![]() ÓėµŲĆę±£³ÖĘ½ŠŠ.ĪŹ±äŠĪĒ°ŗóĮ½ÖįŠÄ
ÓėµŲĆę±£³ÖĘ½ŠŠ.ĪŹ±äŠĪĒ°ŗóĮ½ÖįŠÄ![]() µÄ³¤¶Čӊƻӊ·¢Éś±ä»Æ£æČō²»±ä£¬ĒėŠ“³ö
µÄ³¤¶Čӊƻӊ·¢Éś±ä»Æ£æČō²»±ä£¬ĒėŠ“³ö![]() µÄ³¤¶Č£»Čō±ä»Æ£¬ĒėĒó³ö±ä»ÆĮæ£æ£Ø²Īæ¼Źż¾Ż£ŗ
µÄ³¤¶Č£»Čō±ä»Æ£¬ĒėĒó³ö±ä»ÆĮæ£æ£Ø²Īæ¼Źż¾Ż£ŗ![]() £¬
£¬![]() £¬
£¬![]() £©
£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
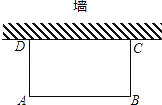
”¾ĢāÄæ”æČēĶ¼£¬ĄūÓĆŅ»ĆęĒ½(Ē½µÄ³¤¶Č²»³¬¹ż45m)£¬ÓĆ80m³¤µÄĄé°ŹĪ§Ņ»øö¾ŲŠĪ³”µŲ£®
(1)ŌõŃłĪ§²ÅÄÜŹ¹¾ŲŠĪ³”µŲµÄĆ껿ĪŖ750m2£æ
(2)ÄÜ·ńŹ¹ĖłĪ§¾ŲŠĪ³”µŲµÄĆ껿ĪŖ810m2 £¬ĪŖŹ²Ć“£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com