练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知:如图,E,F是四边形ABCD的对角线AC上的两点,AF=CE,连接DE,DF,BE,BF.四边形DEBF为平行四边形.求证:四边形ABCD是平行四边形.


    证明：连结BD交AC于点O

    ∵四边形DEBF为平行四边形，∴OD=OB，OE=OF，

    ∵AF=CE,∴AF－EF=CE－EF，即AE=CF，∴AE＋OE=CF＋OF，即OA=OC

    ∴四边形ABCD是平行四边形.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    若实数、满足＜0，＜，则函数的图像可能是（  ）

    A            B            C           D

    查看答案和解析>>

    科目：初中数学 来源： 题型：


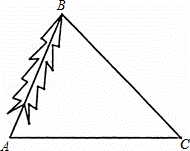
    为了对一棵倾斜的古杉树AB进行保护，需测量其长度．如图，在地面上选取一点C，测得∠ACB=45°，AC=24m，∠BAC=66.5°，求这棵古杉树AB的长度．（结果取整数）

    参考数据：≈1.41，sin66.5°≈0.92，cos66.5°≈0.40，tan66.5°≈2.30．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知反比例函数,则自变量的取值范围是        ;若式子的值为0,则=        

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在平面直角坐标系中,点M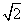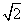（,）,以点M为圆心,OM长为半径作⊙M . 使⊙M与直线OM的另一交点为点B,与轴, 轴的另一交点分别为点D,A（如图）,连接AM.点P是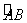上的动点.

    （1）写出∠AMB的度数;

    （2）点Q在射线OP上,且OP·OQ=20,过点Q作QC垂直于直线OM,垂足为C,直线QC交轴于点E.

    ①当动点P与点B重合时,求点E的坐标;

    ②连接QD,设点Q的纵坐标为,△QOD的面积为S.求S与的函数关系式及S的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    将分式方程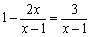去分母，得到正确的整式方程是································ （　　）

    A．1－2x＝3               B．x－1－2x＝3          C．1+2x＝3                 D．x－1+2x＝3

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    研究几何图形，我们往往先给出这类图形的定义，再研究它的性质和判定．

    定义∶六个内角相等的六边形叫等角六边形．

    （1）研究性质

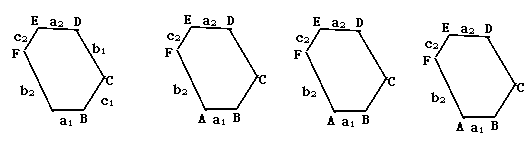
    ①如图1，等角六边形ABCDEF中，三组正对边AB与DE，BC与EF，CD与AF分别有什么位置关系？证明你的结论．

    ②如图2，等角六边形ABCDEF中，如果有AB＝DE，则其余两组正对边BC与EF，CD与AF相等吗？证明你的结论．

    ③如图3，等角六边形ABCDEF中．如果三条正对角线AD，BE，CF相交于一点O，那么三组正对边AB与DE，BC与EF，CD与AF分别有什么数量关系？证明你的结论．

    （2）探索判定

    三组正对边分别平行的六边形，至少需要几个内角为120°才能保证该六变形—定是等角六边形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一个圆柱的底面直径为6cm，高为10cm，则这个圆柱的侧面积是　　cm2（结果保留π）．

    查看答案和解析>>

    同步练习册答案