
【题目】如图,在平面直角坐标系中,边长为3的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,4)经过点O、点C作直线l,将直线l沿y轴上下平移.
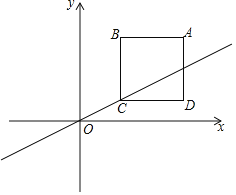
(1)当直线l与正方形ABCD只有一个公共点时,求直线l的解析式;
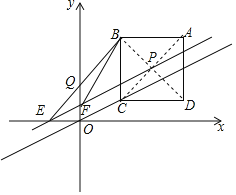
(2)当直线l在平移过程中恰好平分正方形ABCD的面积时,直线l分别与x轴、y轴相交于点E、点F,连接BE、BF,求△BEF的面积.
【答案】(1)y=![]() x+3或y=
x+3或y=![]() x﹣
x﹣![]() ;(2)
;(2)![]()
【解析】
(1)根据题意求得正方形各顶点的坐标,然后根据待定系数法求得直线l的解析式,直线平移,斜率不变,设平移后的直线方程为y=![]() x+b;把点B和D的坐标代入进行解答即可;
x+b;把点B和D的坐标代入进行解答即可;
(2)根据正方形是中心对称图形,当直线l经过对角线的交点时,恰好平分正方形ABCD的面积,求得交点坐标,代入y=![]() x+b,根据待定系数法即可求得直线l的解析式,然后求得E、F的坐标,根据待定系数法求得直线BE的解析式,得到与y轴的交点Q的坐标,根据三角形面积公式即可求得.
x+b,根据待定系数法即可求得直线l的解析式,然后求得E、F的坐标,根据待定系数法求得直线BE的解析式,得到与y轴的交点Q的坐标,根据三角形面积公式即可求得.
(1)∵长为3的正方形ABCD中,点A的坐标为(5,4),
∴B(2,4),C(2,1),D(5,1),
设直线l的解析式为y=kx,
把C(2,1)代入得,1=2k,解得k=![]() ,
,
∴直线l为:y=![]() ,
,
设平移后的直线方程为y=![]() x+b,
x+b,
把点B的坐标代入,得:4=![]() ×2+b,
×2+b,
解得 b=3,
把点D的坐标代入,得:1=![]() ×5+b,
×5+b,
解得: b=﹣![]() ,
,
则平移后的直线l解析式为:y=![]() x+3或y=
x+3或y=![]() x﹣
x﹣![]() ;
;
(2)设AC和BD的交点为P,
∴P点的坐标为(![]() ,
,![]() ),
),
把P点的坐标代入y=![]() x+b得,
x+b得,![]() =
=![]() +b,
+b,
解得b=![]() ,
,
∴此时直线l的解析式为y=![]() x+
x+![]() ,如图,
,如图,
∴E(﹣![]() ,0),F(0,
,0),F(0,![]() ),
),
设直线BE的解析式为:y=mx+n,
则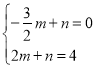 ,解得:
,解得: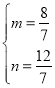 ,
,
∴直线BE的解析式为:y=![]() x+
x+![]() ,
,
∴Q(0,![]() ),
),
∴QF=![]() ﹣
﹣![]() =
=![]() ,
,
∴△BEF的面积=![]() =
=![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的顶点A(-3,0),与y轴交于点B(0,4),在第一象限内有一点P(m,n),且满足4m+3n=12.
(1)求二次函数解析式.
(2)若以点P为圆心的圆与直线AB、x轴相切,求点P的坐标.
(3)若点A关于y轴的对称点为点A′,点C在对称轴上,且2∠CBA+∠PA′O=90.求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC为平行四边形,B、C在⊙O上,A在⊙O外,sin∠OCB=![]() .
.
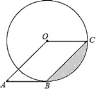
(1)求证:AB与⊙O相切;
(2)若BC=10cm,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解今年九年级学生的数学学习情况,在中考考前适应性训练测试后,对九年级全体同学的数学成绩作了统计分析,按照成绩高低分为A、B、C、D四个等级并绘制了如图1和图2的统计图(均不完整),请结合图中所给出的信息解答问题:
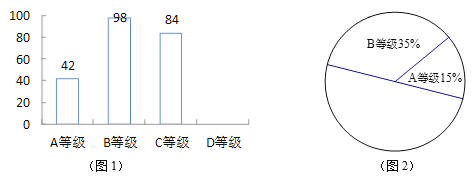
(1)该校九年级学生共有 人.
(2)补全条形统计图与扇形统计图.(要求:请将扇形统计图的空白部分按比例分成两部分.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若整数a使关于x的分式方程![]() =2有整数解,且使关于x的不等式组
=2有整数解,且使关于x的不等式组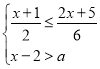 至少有4个整数解,则满足条件的所有整数a的和是( )
至少有4个整数解,则满足条件的所有整数a的和是( )
A.﹣14B.﹣17C.﹣20D.﹣23
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=ax2+bx+c(a≠0,a、b、c为常数)的图像经过点A(-1,0)、B(0,2).
(1)b= (用含有a的代数式表示),c= ;
(2)点O是坐标原点,点C是该函数图像的顶点,若△AOC的面积为1,则a= ;
(3)若x>1时,y<5.结合图像,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 、
、![]() 是弧
是弧![]() (异于
(异于![]() 、
、![]() )上两点,
)上两点,![]() 是弧
是弧![]() 上一动点,
上一动点,![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() .当点
.当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则
时,则![]() 、
、![]() 两点的运动路径长的比是( )
两点的运动路径长的比是( )
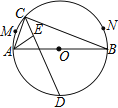
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地2016年为做好“精准扶贫”,投入资金1000万元用于异地安置,并规划投入资金逐年增加,2018年在2016年的基础上增加投入资金1250万元.
(1)从2016年到2018年,该地投入异地安置资金的年平均增长率为多少?
(2)在2018年异地安置的具体实施中,该地计划投入资金不低于400万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天补助5元,按租房400天计算,试求今年该地至少有多少户享受到优先搬迁租房奖励?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com