
【题目】关于x的方程组![]() 的解满足x为负数,y为正数,
的解满足x为负数,y为正数,
(1)求 k的取值范围.
(2)化简|k+5|+|k-3|
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②a﹣b+c<0;③4a+b+c=0;④抛物线的顶点坐标为(2,b);⑤当x<1时,y随x增大而增大.其中结论正确的是( )
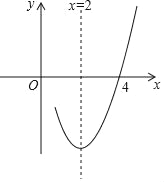
A. ①②③ B. ①④⑤ C. ①③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017湖北省十堰市,第10题,3分)如图,直线![]() 分别交x轴,y轴于A,B,M是反比例函数
分别交x轴,y轴于A,B,M是反比例函数![]() (x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,ACBD=
(x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,ACBD=![]() ,则k的值为( )
,则k的值为( )
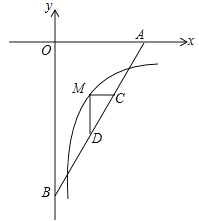
A. ﹣3 B. ﹣4 C. ﹣5 D. ﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图中的小方格都是边长为1的正方形, △ABC与△A′ B′ C′是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.

(1)画出位似中心点0;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点0为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明.如图,已知AB∥CD,∠B=∠C,
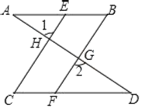
求证:∠1=∠2.
证明:∵AB∥CD(已知)
∴∠B= ( ).
∵∠B=∠C(已知)
∴∠BFD=∠C(等量代换)
∴EC∥ ( )
∴∠2= (两直线平行,同位角相等)
∵∠1= ( )
∴∠1=∠2(等量代换).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,

(1)若把△ABC向右平移2个单位,再向下平移3个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(2)如果在第二象限内有一点P(m,3),四边形ACOP的面积为 (用含m的式子表示)
(3)在(2)的条件下,是否存在点P,使四边形ACOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校设计了如图所示的雕塑,取名“阶梯”, 现在工厂师傅打算用油漆喷刷所有暴露面,经测量,已知每个小立方体的棱长为0.5米.

(1)请你画出从它的正面、左面、上面三个不同方向看到的平面图形.
(2)请你帮助工人师傅计算一下,需要喷刷油漆的总面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图,灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a度/秒,灯B转动的速度是b度/秒,且a,b满足|a﹣3b﹣1|+(a+b﹣5)2=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°.
(1)求a,b的值;
(2)若两灯同时转动,经过42秒,两灯射出的光束交于C,求此时∠ACB的度数;
(3)若灯B射线先转动10秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?(直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:如图,点A、B在数轴上分别表示有理数a、b,则A、B两点之间的距离可以表示为|a﹣b|.
根据阅读材料与你的理解回答下列问题:
(1)数轴上表示3与﹣2的两点之间的距离是 .
(2)数轴上有理数x与有理数7所对应两点之间的距离用绝对值符号可以表示为 .
(3)代数式|x+8|可以表示数轴上有理数x与有理数 所对应的两点之间的距离;若|x+8|=5,则x= .
(4)求代数式|x+1008|+|x+504|+|x﹣1007|的最小值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com