
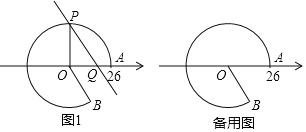
����Ŀ����ͼ����A�������϶�Ӧ����Ϊ26����ԭ��OΪԲ�ģ�OAΪ�뾶���Ż�![]() ��ʹ��B��O���·�����tan��AOB=
��ʹ��B��O���·�����tan��AOB=![]() �����Ż�
�����Ż�![]() ����ȡһ��P�����ܹ�P��ֱ��l��OB�������ڵ�Q����Q�������϶�Ӧ����Ϊx������OP��
����ȡһ��P�����ܹ�P��ֱ��l��OB�������ڵ�Q����Q�������϶�Ӧ����Ϊx������OP��
��1�����Ż���һ��![]() �ij�Ϊ13�������AOP�Ķ�����x��ֵ��
�ij�Ϊ13�������AOP�Ķ�����x��ֵ��
��2����x����Сֵ����ָ����ʱֱ��l��![]() ����Բ��λ�ù�ϵ��
����Բ��λ�ù�ϵ��
��3�����߶�PQ�ij�Ϊ12.5��ֱ��д����ʱx��ֵ��
���𰸡���1����POA=90�㣬x=![]() ����2����ֱ��PQ���O����ʱʱ����ʱx��ֵΪ��32.5����3������������x��ֵΪ��16.5��31.5��31.5��
����2����ֱ��PQ���O����ʱʱ����ʱx��ֵΪ��32.5����3������������x��ֵΪ��16.5��31.5��31.5��
����������1�����û�����ʽ���Բ�ĽǼ��ɽ�����⣻
��2����ͼ��ֱ��PQ���O����ʱʱ��x��ֵ��С��
��3������P���Ż�![]() �ϵ�����һ�㣬����P���λ�÷��������Σ��ֱ���⼴�ɽ�����⣮
�ϵ�����һ�㣬����P���λ�÷��������Σ��ֱ���⼴�ɽ�����⣮
��1����ͼ1�У�
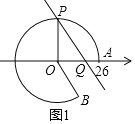
��![]() =13��
=13�У�
���n=90�㣬
���POQ=90�㣬
��PQ��OB��
���PQO=��BOQ��
��tan��PQO=tan��QOB=![]() ��
��
��OQ=![]() ��
��
��x=![]() ��
��
��2����ͼ��ֱ��PQ���O����ʱʱ��x��ֵ��С��

��Rt��OPQ��OQ=OP��![]() =32.5��
=32.5��
��ʱx��ֵΪ��32.5��
��3�������������
����ͼ2�У���OH��PQ��H����OH=4k��QH=3k��

��Rt��OPH����OP2=OH2+PH2��
��262=��4k��2+��12.5��3k��2��
�����ã�k2��3k��20.79=0��
���k=6.3��3.3����������
��OQ=5k=31.5��
��ʱx��ֵΪ31.5��
����ͼ3�У���OH��PQ��PQ���ӳ�����H����OH=4k��QH=3k��

��Rt����Rt��OPH����OP2=OH2+PH2��
��262=��4k��2+��12.5+3k��2��
�����ã�k2+3k��20.79=0��
���k=��6.3����������3.3��
��OQ=5k=16.5��
��ʱx��ֵΪ��16.5��
����ͼ4�У���OH��PQ��H����OH=4k��AH=3k��

��Rt��OPH����OP2=OH2+PH2��
��262=��4k��2+��12.5��3k��2��
�����ã�k2��3k��20.79=0��
���k=6.3��3.3����������
��OQ=5k=31.5��������������
��ʱx��ֵΪ��31.5��
��������������������x��ֵΪ��16.5��31.5��31.5��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
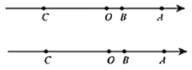
����Ŀ����ͼ����֪�����ϵ�![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ����
����![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ��
��![]() ��������һ�㣬��
��������һ�㣬��![]() ������
������![]() �ӵ�
�ӵ�![]() ��������ÿ��
��������ÿ��![]() ����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊ
����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊ![]() �룮
�룮
��1�������ϵ�![]() ��ʾ����Ϊ �����ú�
��ʾ����Ϊ �����ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��![]() ����ʾ����Ϊ ��
����ʾ����Ϊ ��
��2����![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() ���е㣬��
���е㣬��![]() ���˶������У��߶�
���˶������У��߶�![]() �ij����Ƿ����仯�����仯����˵�����ɣ������䣬���߶�
�ij����Ƿ����仯�����仯����˵�����ɣ������䣬���߶�![]() �ij��ȣ�
�ij��ȣ�
��3������![]() �ӵ�
�ӵ�![]() ��������ÿ��
��������ÿ��![]() ����λ���ȵ��ٶ����������������˶�������
����λ���ȵ��ٶ����������������˶�������![]() �ӵ�
�ӵ�![]() �������Ե�ÿ��
�������Ե�ÿ������λ�������������������˶�����
![]() ����ͬʱ���������˶������У�
����ͬʱ���������˶������У�![]() ��
��![]() �ľ��룬
�ľ��룬![]() ��
��![]() �����У��Ƿ���������ξ�����ȵ�ʱ�����У��������ʱ��ֵ����û�У���˵�����ɣ�
�����У��Ƿ���������ξ�����ȵ�ʱ�����У��������ʱ��ֵ����û�У���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijһ���һ�������Թ�¥Ϊ�������ڶ���������Ӫ������Ϊ����������Ϊ�����г���̣���λ��km�����Ⱥ�����¼���£�![]() .
.
��1�������һ���˿��͵�Ŀ�ĵأ�������¥�������Զ���ڹ�¥��ʲô����
��2����ÿǧ�ļ۸�Ϊ2.4Ԫ��˾��һ�������Ӫҵ���Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��������![]() ��
��![]() ��
��![]() �������ϵĶ�Ӧ����ͼ��ʾ���������ʽ��
�������ϵĶ�Ӧ����ͼ��ʾ���������ʽ��![]()
![]()
��2������ij����������һ�ܴ���������������Ϊ210�֣��ƻ�ÿ�촦��30�֣����ڸ���ԭ��ʵ��ÿ�촦������ƻ�����г��룬ij�������ʵ�ʴ��������¼���£�
+6��-3��+4��-1��+2��-5��0
����������һ��ʵ�ʴ������������Ƕ��ٶ֣�
������������ʵ�м������ʣ�ÿ����һ������������300Ԫ��ͬʱ�ֹ涨�����һ���������⽱100Ԫ���겻��������ٴ���һ�������100Ԫ����ô�ó�������һ�ܵĹ����ܶ��Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ��Ӧ��������٣���������ؽ�������Ҫ��ȾԴ��������ˮ���ؽ�������Ⱦ���ŷţ��ֱ��ü������ҷ�����������������ˮ��Ⱦָ����ΪQ���ؽ��������ҷ�������һ���������������깤�����ӵ��꿪ʼ����������ÿ�ҹ���һ�꽵�͵�Qֵƽ��Ϊ0.3����һ����40�ҹ������ҷ����������������������������ؽ�ˮ�����Ը��ƣ�
��1����һ��40�ҹ������ҷ�������һ�꽵�͵�QֵΪ______��
��2���ӵڶ�����ÿ�����ҷ����������Ĺ�����������һ�궼�����ӣ����������������ҷ������������Ĺ��������ǵڶ������������ҷ����������Ĺ���������1.5�������������ҷ������������͵�QֵΪ57����ڶ������������ҷ����������Ĺ�������Ϊm�ң����������������ҷ����������Ĺ�������Ϊn�ң�
�����г�����m��n�ķ����飬����⣻
�ڸ���������ˮ�ü�����������һ�꽵�͵�QֵΪ20.5���ӵڶ�����ÿ�������͵�Qֵ����һ�궼����a�����������ü������ַ������������͵�Qֵ�ȵڶ����ü������ַ������������͵�Qֵ��32����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
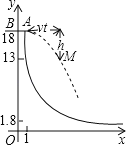
����Ŀ����ͼ���ֻ����صĽ���ʾ��ͼ��ƽ̨AB��x�ᣨˮƽ��18�ף���y�ύ�ڵ�B���뻬��y=![]() ��x��1�����ڵ�A����AB=1�ף��˶�Ա�����ɵ㣩��BA�������ٶ�v��/���A�������·�������M������·�ߵ�ijλ�ã����Կ���������ʵ�������M��A����ֱ����h���ף���ɳ�ʱ��t���룩��ƽ�������ȣ���t=1ʱh=5��M��A��ˮƽ������vt�ף�
��x��1�����ڵ�A����AB=1�ף��˶�Ա�����ɵ㣩��BA�������ٶ�v��/���A�������·�������M������·�ߵ�ijλ�ã����Կ���������ʵ�������M��A����ֱ����h���ף���ɳ�ʱ��t���룩��ƽ�������ȣ���t=1ʱh=5��M��A��ˮƽ������vt�ף�
��1����k������t��ʾh��
��2����v=5����t��ʾ��M�ĺ�����x��������y������y��x�Ĺ�ϵʽ����дx��ȡֵ��Χ������y=13ʱ�˶�Ա�����·���������ֱ���룻
��3�����˶�Ա�ס���ͬʱ��A���ɳ����ٶȷֱ���5��/�롢v����/�룮����x��1.8�ף�����λ�ڼ��Ҳ೬��4.5��λ��ʱ��ֱ��д��t��ֵ��v���ķ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC���A'B'C��ƽ��ֱ������ϵ�е�λ����ͼ��

��1���ֱ�д��B��B'�����꣺B______��B��______��
��2������P��a��b���ǡ�ABC�ڲ�һ�㣬��ƽ�ƺ��A'B'C�ڵĶ�Ӧ��P�������Ϊ______��
��3�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ҹ��Ƿܶ������������������ϣ���C��A�ľ���պ���3����C�����A�����Ҹ���������C��A��B�ľ���֮��Ϊ6����C����A��B�����Ҹ�������
��1����ͼ1����A��ʾ����Ϊ��1����A���Ҹ���C����ʾ����Ӧ������ ����
��2����ͼ2��M��NΪ���������㣬��M����ʾ����Ϊ4����N����ʾ����Ϊ��2����C����M��N���Ҹ����ģ���C����ʾ������������ ������һ�����ɣ���
��3����ͼ3��A��B��PΪ���������㣬��A����ʾ����Ϊ��1����B����ʾ����Ϊ4����P����ʾ����Ϊ8������һֻ�������ϴӵ�P��������2����λÿ����ٶ������˶���������������ʱ������������A��B���Ҹ����ģ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ڷ�ѧ·�ϣ����������Ϸ���һ���������й������Dz�����������ֱ������CD������A���ñ����ƶ���D��������Ϊ42�������������B���ĸ���Ϊ30�㣨B��C��D��ͬһ��ֱ���ϣ���AB=10m��������6.5m����BC=65m�����������CD�ij����������С�����һλ�������ο����ݣ�sin42���0.67��cos42���0.74��tan42���0.90��![]() ��1.73��
��1.73��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com