
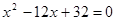 的两根,且
的两根,且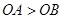 。请解答下列问题:
。请解答下列问题:
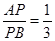 ,求过点P的反比例函数的解析式。
,求过点P的反比例函数的解析式。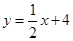 ;(2)
;(2)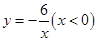
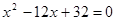 ,即可求得点A与B的坐标,然后利用待定系数法即可求得直线AB的解析式;
,即可求得点A与B的坐标,然后利用待定系数法即可求得直线AB的解析式;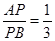 ,利用平行线分线段成比例定理,即可求得AH的长,则可求得点P的横坐标,代入一次函数解析式,即可求得点P的坐标,再利用待定系数法即可求得过点P的反比例函数的解析式.
,利用平行线分线段成比例定理,即可求得AH的长,则可求得点P的横坐标,代入一次函数解析式,即可求得点P的坐标,再利用待定系数法即可求得过点P的反比例函数的解析式.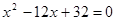
 ,解得
,解得 ,
,
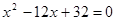 的两根,且
的两根,且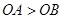 ,
, ,解得
,解得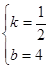
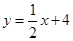 ;
;

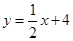 上,
上, ×(-6)+4=1.
×(-6)+4=1.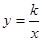
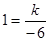 ,解得
,解得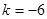
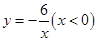 .
.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
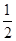 x2+mx+n交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的横坐标是-3,点B的横坐标是1.
x2+mx+n交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的横坐标是-3,点B的横坐标是1.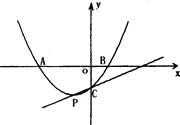
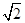 ≈1.41,
≈1.41, ≈1.73,
≈1.73, ≈2.24)
≈2.24) 查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
| 弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com