
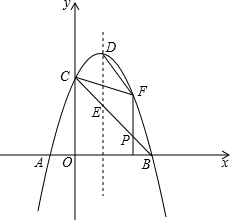
 ��ͼ��������y=-x2+2x+3��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y���ཻ��C�㣬����ΪD��
��ͼ��������y=-x2+2x+3��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y���ཻ��C�㣬����ΪD������ ��1���������߽���ʽ��y=0���ó�����x��һԪ���η��̣��ⷽ�̼��ɵó����ۣ�
��2�����������߽���ʽ��x=0���yֵ�����ɵó���C�����꣬��ϵ�B��C���������ô���ϵ�������ֱ��BC�Ľ���ʽ�����ɵ�P�ĺ�����Ϊm�ҳ���F��P�����꣬�ɴ˼��ɵó����ۣ�
�������䷽����������ߵĶԳ����Լ�����D�����꣬���ݵ�D���꼴�ɵó���E�����Լ��߶�DE�ij��ȣ��ٸ���ƽ���ı��ε����ʿɵó�DE=PF���ɴ˿ɵó�����m��һԪ���η��̣��ⷽ�̼��ɵó����ۣ�
����PF��x��ɵó���Ҫ��PCFΪֱ�������Σ����CFP=90����PCF=90�㣮����CFP=90��ʱ���ɵó���C��F���ڶԳ���Գƣ����ݵ�C�������Լ������߶Գ���Ľ���ʽ���ɵó�mֵ������PCF=90��ʱ��ϵ�B��C������ɵó���PCFΪ����ֱ�������Σ����ݵ���ֱ�������ε����ʼ��ɵó�����m�ķ��̣���֮���ɵó�m��ֵ�����ϼ��ɵó����ۣ�
��� �⣺��1����y=-x2+2x+3��y=0��
����-x2+2x+3=��3-x����x+1��=0��
��ã�x1=-1��x2=3��
�ߵ�A�ڵ�B����࣬
���A��-1��0������B��3��0����
��2������y=-x2+2x+3��x=0����y=3��
���C��0��3����
��ֱ��BC�Ľ���ʽΪy=kx+b��
����B��3��0����C��0��3������y=kx+b��
�ã�$\left\{\begin{array}{l}{0=3k+b}\\{3=b}\end{array}\right.$����ã�$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪy=-x+3��
�ߵ�P�ĺ�����Ϊm��PF��x�ᣬ
���P��m��-m+3����F��m��-m2+2m+3����
��PF=-m2+2m+3-��-m+3��=-m2+3m��0��m��3����
�ڡ�y=-x2+2x+3=-��x-1��2+4��
�������ߵĶԳ���Ϊx=1������D��1��4����
��x=1����y=-x+3�У��ã�y=2��
���E��1��2����
��DE=4-2=2��
���ı���PEDFΪƽ���ı��Σ�
��DE=PF����2=-m2+3m��
��ã�m1=1����ȥ����m2=2��
�൱m=2ʱ���ı���PEDFΪƽ���ı��Σ�
�ۡ�PF��x�ᣬ
���CPF��90�㣬
��Ҫ��PCFΪֱ�������Σ����CFP=90����PCF=90�㣮
��i������CFP=90��ʱ��
��PF��x�ᣬ��CFP=90�㣬
��CF��x�ᣬ
���C��F���ڶԳ���Գƣ�
�ߵ�C��0��3���������߶Գ���Ϊx=1��
��m=2��
��ii������PCF=90��ʱ��
�ߵ�B��3��0������C��0��3������PCF=90�㣬
���CPF=��OCB=45�㣬
���PCFΪ����ֱ�������Σ�
��PF=$\sqrt{2}$CP=-m2+3m=2m��
��ã�m=1��m=0����ȥ����
������������mΪ1��2ʱ����PCFΪֱ�������Σ�
���� ���⿼���˽�һԪ���η��̡�����ϵ������������ʽ��ƽ���ı��ε������Լ�ֱ�������ε����ʣ�����Ĺؼ��ǣ���1�������x��һԪ���η��̣���2�������ֱ��BC�Ľ���ʽ���ڸ���ƽ���ı��ε������ҳ�����m��һԪ���η��̣��۸��ݶ��κ����ĶԳ��ԣ�����ֱ�������ε����ʣ�������⣮���������е��⣬�ѶȲ������������Ŀʱ������һ�Σ�����Σ�����ͼ���ϵ�����������ҳ���������ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | 3 | C�� | 4 | D�� | -4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
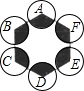 ��ͼ���������εı߳�Ϊ10���ֱ����������εĶ���A��B��C��D��E��FΪԲ�ģ���6��ȫ�ȵ�Բ����Բ�İ뾶Ϊx����0��x��5����Ӱ���ֵ����Ϊy���ܷ�ӳy��x֮�亯����ϵ�Ĵ���ͼ���ǣ�������
��ͼ���������εı߳�Ϊ10���ֱ����������εĶ���A��B��C��D��E��FΪԲ�ģ���6��ȫ�ȵ�Բ����Բ�İ뾶Ϊx����0��x��5����Ӱ���ֵ����Ϊy���ܷ�ӳy��x֮�亯����ϵ�Ĵ���ͼ���ǣ�������| A�� | 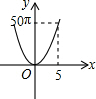 | B�� | 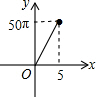 | C�� | 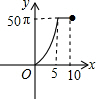 | D�� | 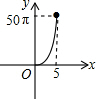 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | ��λ�� | C�� | ƽ���� | D�� | ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
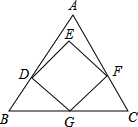 һ�������κ�һ���ȱ������ε�λ����ͼ��ʾ�ڷţ���G��BC�е㣬�����ζԽ���EG��BC�����AFE=��������
һ�������κ�һ���ȱ������ε�λ����ͼ��ʾ�ڷţ���G��BC�е㣬�����ζԽ���EG��BC�����AFE=��������| A�� | 10�� | B�� | 15�� | C�� | 20�� | D�� | 25�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��һֻ������ij����λ��ƽ��ͼ�����У��������ų������ر�ƫ��60��ķ�������400cm��������ͤ��������ͤͣ��Ƭ�̣�С�������ر�ƫ��60��ķ�������400cm�������Ĺ㳡��
��ͼ��һֻ������ij����λ��ƽ��ͼ�����У��������ų������ر�ƫ��60��ķ�������400cm��������ͤ��������ͤͣ��Ƭ�̣�С�������ر�ƫ��60��ķ�������400cm�������Ĺ㳡���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
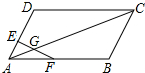 ��ͼ����EΪ?ABCD��AD����һ�㣬��AE��ED=1��3����FΪAB���е㣬EF��AC�ڵ�G����AG��GC����1��5��
��ͼ����EΪ?ABCD��AD����һ�㣬��AE��ED=1��3����FΪAB���е㣬EF��AC�ڵ�G����AG��GC����1��5���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com