
 如图,某大街水平地面有两根路灯灯杆AB=CD=10m,小明晚上站在两灯杆的正中位置观察自己眼睛处影子的俯角∠MEG=∠NEH=11.31°,已知地面到小明眼睛处的高度EF=1.5m.
如图,某大街水平地面有两根路灯灯杆AB=CD=10m,小明晚上站在两灯杆的正中位置观察自己眼睛处影子的俯角∠MEG=∠NEH=11.31°,已知地面到小明眼睛处的高度EF=1.5m.分析 (1)由∠EHG=∠NEH=11.31°,分别在Rt△ABH与Rt△EFH中,利用三角函数的知识即可求得BH与FH的长,继而求得答案;
(2)首先设休闲街长x米,则购物街长为(760-x)米,根据题意列出方程,解方程求得答案.
解答 解:解:(1)∵MN∥BD,
∴∠EHG=∠NEH=11.31°,
∴在Rt△ABH中,BH=$\frac{AB}{tan11.31°}$≈$\frac{10}{0.20}$=50(米),
在Rt△EFH中,FH=$\frac{EF}{tan11.31°}$≈$\frac{1.5}{0.20}$=7.5(米),
∴BF=BH-FH=42.5(米),
∴DB=2BF=85(米);
答:两灯秆的距离DB为85米;
(2)设休闲街长x米,则购物街长为(760-x)米,
$\frac{x}{85}$+$\frac{760-x}{85-35}$=12-1,
解得:x=510,
760-510=250(米),
答:休闲街和购物街分别长510米,250米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题以及一元一次方程的应用,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | $\frac{1}{2}$ | C. | 2 | D. | $\frac{11}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
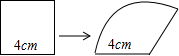 手工课上,小明将一个边长为4cm的正方形铁丝框,变形成为如图所示一个扇形框,周长不变,且扇形框半径等于正方形的边长,则该扇形的面积大小为16cm2.
手工课上,小明将一个边长为4cm的正方形铁丝框,变形成为如图所示一个扇形框,周长不变,且扇形框半径等于正方形的边长,则该扇形的面积大小为16cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1-(1-x)=1 | B. | 1+(1-x)=1 | C. | 1-(1-x)=x-2 | D. | 1+(1-x)=x-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9.16×103克 | B. | 9.16×104克 | C. | 9,16×105克 | D. | 0.916×105克 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com