
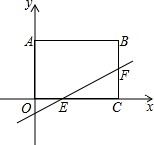
 如图,在平面直角坐标系中,直线y=$\frac{2}{3}$x-$\frac{2}{3}$与矩形ABCO的边OC、BC分别交于点E、F,已知OA=3,OC=4,则△CEF的面积是3.
如图,在平面直角坐标系中,直线y=$\frac{2}{3}$x-$\frac{2}{3}$与矩形ABCO的边OC、BC分别交于点E、F,已知OA=3,OC=4,则△CEF的面积是3. 分析 根据直线解析式分别求出点E、F的坐标,然后利用三角形的面积公式求解即可.
解答 解:∵当y=0时,$\frac{2}{3}$x-$\frac{2}{3}$=0,解得x=1,
∴点E的坐标是(1,0),即OE=1,
∵OC=4,
∴EC=OC-OE=4-1=3,
∴点F的横坐标是4,
∴y=$\frac{2}{3}$×4-$\frac{2}{3}$=2,即CF=2,
∴△CEF的面积=$\frac{1}{2}$×CE×CF=$\frac{1}{2}$×3×2=3
故答案为:3.
点评 本题考查的是一次函数图象上点的坐标特点,根据直线的解析式求出点E、F的坐标是解题的关键,同时也考查了矩形的性质,难度不大.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
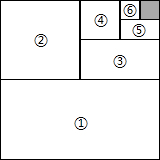 如图,将一个边长为1的正方形纸片分割成7个部分,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推.
如图,将一个边长为1的正方形纸片分割成7个部分,部分②是部分①面积的一半,部分③是部分②面积的一半,依此类推.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
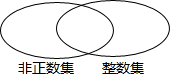 如图的两个圈分别表示非正数集和整数集,请在每个圈内填入六个数,其中三个数既在非正数集又在整数集内,你能用一个合适的语句来表示两个圈重叠部分的意义吗?
如图的两个圈分别表示非正数集和整数集,请在每个圈内填入六个数,其中三个数既在非正数集又在整数集内,你能用一个合适的语句来表示两个圈重叠部分的意义吗?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
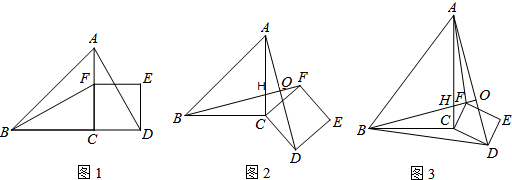
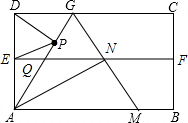 如图,四边形ABCD是矩形纸片,AD=2$\sqrt{3}$,对折矩形纸片ABCD,使AB与CD重合,折痕为EF;展平后再过点A折叠矩形纸片,使点D落在EF上的点N,折痕AG与EF相交于点Q;再次展平,连接AN,GN,延长GN交AB于点M,有如下结论:
如图,四边形ABCD是矩形纸片,AD=2$\sqrt{3}$,对折矩形纸片ABCD,使AB与CD重合,折痕为EF;展平后再过点A折叠矩形纸片,使点D落在EF上的点N,折痕AG与EF相交于点Q;再次展平,连接AN,GN,延长GN交AB于点M,有如下结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
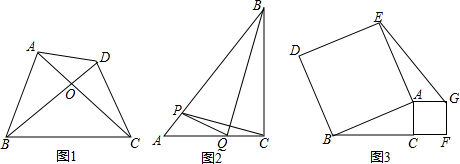
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com