
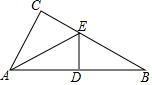
 如图:已知,∠C=90°,AD=AC,DE⊥AB交BC于点E.若∠B=40°,则∠EAC=25°.
如图:已知,∠C=90°,AD=AC,DE⊥AB交BC于点E.若∠B=40°,则∠EAC=25°. 分析 根据∠C=90°AD=AC,求证△CAE≌△DAE,∠CAE=∠DAE=$\frac{1}{2}$∠CAB,再由∠C=90°,∠B=40°,求出∠EAC的度数,然后即可求出∠AEC的度数.
解答 解:∵在△ABC中,∠C=90°,
AD=AC,DE⊥AB交BC于点E,
在Rt△CAE与△RtDAE中,
$\left\{\begin{array}{l}{AC=AD}\\{AE=AE}\end{array}\right.$,
∴Rt△CAE≌Rt△DAE(HL),
∴∠CAE=∠DAE=$\frac{1}{2}$∠CAB,
∵∠B+∠CAB=90°,∠B=40°,
∴∠CAB=90°-40°=50°,
∴∠EAC=25°.
故答案为:25.
点评 此题主要考查学生对直角三角形全等的判定和三角形内角和定理的理解和掌握,解答此题的关键是求证△CAE≌△DAE,此题稍微有点难度,属于中档题.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:选择题
| A. | 4种 | B. | 3种 | C. | 2种 | D. | 1种 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
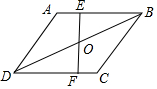 如图,在菱形ABCD中,∠C=120°,FE⊥AB于点E,并交BD于点O,恰好O是BD的中点,若AD=6,则四边形AEFD的周长为( )
如图,在菱形ABCD中,∠C=120°,FE⊥AB于点E,并交BD于点O,恰好O是BD的中点,若AD=6,则四边形AEFD的周长为( )| A. | 12+$\frac{3}{2}$$\sqrt{3}$ | B. | 12+3$\sqrt{3}$ | C. | 15 | D. | 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com