
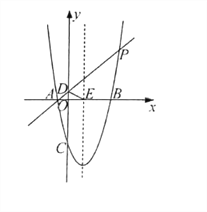
【题目】已知抛物线y=a(x-2)2-9经过点P(6,7),与x轴交于A、B两点,与y轴交于点C,直线AP与y轴交于点D,抛物线对称轴与x轴交于点E.
(1)求抛物线的解析式;
(2)过点E任作一条直线l(点B、C分别位于直线l的异侧),设点C到直线的距离为m,点B到直线l的距离为n,求m+n的最大值;
(3)y轴上是否存在点Q,使∠QPD=∠DEO,若存在,请求出点Q的坐标:若不存在,请说明理由.
【答案】(1) y=x2-4x-5;(2)![]() ;(3)Q1(0,5),Q2(0,-11).
;(3)Q1(0,5),Q2(0,-11).
【解析】分析:(1)把P点坐标代入y=a(x-2)2-9中求出a即可得到抛物线解析式;
(2)作BM⊥l于M,BN⊥l于N,BG⊥CM于G,如图1,利用四边形BGMN为矩形得到BN=MG,则m+n=CG,利用BG≤BC(当且仅当M点在BC上取等号)得到m+n的最大值为BC的长,然后求出B、C坐标后计算出BC即可;
(3)先利用待定系数法求出直线AD的解析式为y=x+1,则D(0,1),PD=6![]() ,△AOD为等腰直角三角形,易得E(2,0),则tan∠DEO=
,△AOD为等腰直角三角形,易得E(2,0),则tan∠DEO=![]() ,讨论:当点Q在点D的上方,作QG⊥AP于G,如图2,设QG=t,证明△QDG为等腰直角三角形得到DG=QG=t,QD=
,讨论:当点Q在点D的上方,作QG⊥AP于G,如图2,设QG=t,证明△QDG为等腰直角三角形得到DG=QG=t,QD=![]() t,则利用∠QPD=∠DEO和正切定义得到
t,则利用∠QPD=∠DEO和正切定义得到![]() ,解方程求出t,从而可确定Q点坐标;当点Q在点D的下方,作QG⊥AP于G,如图3,设QG=t,利用同样方法得到
,解方程求出t,从而可确定Q点坐标;当点Q在点D的下方,作QG⊥AP于G,如图3,设QG=t,利用同样方法得到![]() ,然后解方程求出t,从而得到Q点坐标.
,然后解方程求出t,从而得到Q点坐标.
详解:(1)∵抛物线y=a(x-2)2-9经过点P(6,7),
∴a(6-2)2-9=7,解得a=1,
∴抛物线解析式为y=(x-2)2-9,
即y=x2-4x-5;
(2)作BM⊥l于M,BN⊥l于N,BG⊥CM于G,如图1,
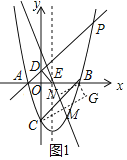
易得四边形BGMN为矩形,
∴BN=MG,
∴m+n=CM+BN=CM+MG=CG,
∵BG≤BC(当且仅当M点在BC上取等号)
∴m+n的最大值为BC的长,
当x=0时,y=x2-4x-5=-5,则C(0,-5),
当y=0时,x2-4x+5=0,解得x1=-1,x2=5,则A(-1,0),B(5,0)
∴BC=![]() ,
,
∴m+n的最大值为5![]() ;
;
(3)存在.
设直线AD的解析式为y=kx+b,
把A(-1,0),P(6,7)代入得![]() ,
,
解得![]() ,
,
∴直线AD的解析式为y=x+1,
当x=0,y=x+1=1,则D(0,1),
∴PD=![]() ,△AOD为等腰直角三角形,
,△AOD为等腰直角三角形,
∵抛物线的对称轴为直线x=2,
∴E(2,0),
∴tan∠DEO=![]() ,
,
当点Q在点D的上方,作QG⊥AP于G,如图2,
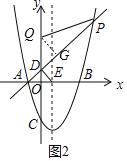
设QG=t,
∵∠QDG=∠ADO=45°,
∴△QDG为等腰直角三角形,
∴DG=QG=t,QD=![]() QG=
QG=![]() t,
t,
∴PG=PD-DG=6![]() -t,
-t,
∵∠QPD=∠DEO,
∴tan∠QPD=![]() ,
,
∴![]() ,解得t=2
,解得t=2![]() ,
,
∴DQ=2![]() ×
×![]() =4,
=4,
∴OQ=4+1=5,
∴Q点坐标为(0,5);
当点Q在点D的下方,作QG⊥AP于G,如图3,
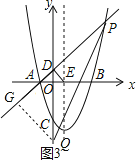
设QG=t,
∴△QDG为等腰直角三角形,
∴DG=QG=t,QD=![]() QG=
QG=![]() t,
t,
∴PG=PD+DG=6![]() +t,
+t,
∵∠QPD=∠DEO,
∴tan∠QPD=![]() ,
,
∴![]() ,解得t=6
,解得t=6![]() ,
,
∴DQ=6![]() ×
×![]() =12,
=12,
∴OQ=12-1=11
∴Q点坐标为(0,-11),
综上所述,Q点的坐标为(0,5)或(0,-11).


科目:初中数学 来源: 题型:
【题目】阅读下面的证明过程,指出其错误.(在错误部分下方划线)已知△ABC,求证:∠A+∠B+∠C=180°
(1)证明:过A作DE∥BC,且使∠1=∠C
∵DE∥BC(作图)
∴∠2=∠B(内错角相等两直线平行)
∵∠1=∠C(作图)
∴∠B+∠C+∠3=∠2+∠1+∠3(等量代换)
∠2+∠l+∠3=180°(周角的定义)
即∠BAC+∠B+∠C=180°(等量代换)
(2)类比探究:请同学们参考图2,模仿(1)的解决过程,避免(1)中的错误,试说明求证:∠A+∠B+∠C=180°
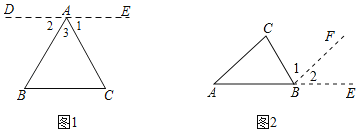
查看答案和解析>>
科目:初中数学 来源: 题型:
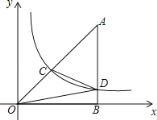
【题目】如图,△OAB中,∠ABO=90°,点A位于第一象限,点O为坐标原点,点B在x轴正半轴上,若双曲线y=![]() (x>0)与△OAB的边AO、AB分别交于点C、D,点C为AO的中点,连接OD、CD.若S△OBD=3,则S△OCD为( )
(x>0)与△OAB的边AO、AB分别交于点C、D,点C为AO的中点,连接OD、CD.若S△OBD=3,则S△OCD为( )
A.3B.4C.![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=2x的图象与反比例函数y=![]() (x>0),y=
(x>0),y=![]() (x>0)的图象分别交于P,Q两点,点P为OQ的中点,Rt△ABC的直角顶点A是双曲线y=
(x>0)的图象分别交于P,Q两点,点P为OQ的中点,Rt△ABC的直角顶点A是双曲线y=![]() (x>0)上一动点,顶点B,C在双曲线y=
(x>0)上一动点,顶点B,C在双曲线y=![]() (x>0)上,且两直角边均与坐标轴平行.
(x>0)上,且两直角边均与坐标轴平行.
(1)直接写出k的值;
(2)△ABC的面积是否变化?若不变,求出△ABC的面积;若变化,请说明理由;
(3)直线y=2x是否存在点D,使得以A,B,C,D为顶点的四边形是平行四边形,若存在,求出点A的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
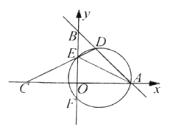
【题目】如图,在平面内直角坐标系中,直线y=-x+6分别于x轴、y轴交于A、B两点,点C与点A关于y轴对称,点E为线段OB上一动点(不与O、B重合),CE的延长线与AB交于点D,过A、D、E三点的圆与y轴交于点F
(1)求A、B、C三点的坐标
(2)求证:BE·EF=DE·AE
(3)若tan∠BAE=![]() ,求点F的坐标
,求点F的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
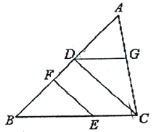
【题目】将下面的证明过程补充完整,括号内写上相应理由或依据:已知,如图,![]() ,
,![]() ,垂足分别为D、F,
,垂足分别为D、F,![]() ,请试说明
,请试说明![]() .
.
证明:∵![]() ,
,![]() (已知)
(已知)
∴![]() (____________________________)
(____________________________)
∴![]() ________(____________________________)
________(____________________________)
∴![]() ________(____________________________)
________(____________________________)
又∵![]() (已知)
(已知)
∴![]() ________(____________________________)
________(____________________________)
∴![]() ________(____________________________)
________(____________________________)
∴![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,以O为圆心的半圆分别与AB、AC边相切于D、E两点,且O点在BC边上,则图中阴影部分面积S阴等于( )

A. ![]() B.
B. ![]() C. 5-
C. 5-![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com