练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．如果$\frac{6sinα-2cosα}{2sinα+cosα}$=2，那么tanα=（　　）
    A．2B．1C．$\frac{1}{2}$D．4

    分析 原式去分母得6sinα-2cosα=4sinα+2cosα，整理后可得sinα=2cosα，由tanα=$\frac{sinα}{cosα}$可得．

    解答 解：由$\frac{6sinα-2cosα}{2sinα+cosα}$=2得：6sinα-2cosα=4sinα+2cosα，
    整理，得：sinα=2cosα，
    两边都除以cosα，得：$\frac{sinα}{cosα}$=2，即tanα=2，
    故选：A．

    点评 本题主要考查锐角三角函数的定义，掌握tanα=$\frac{sinα}{cosα}$是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

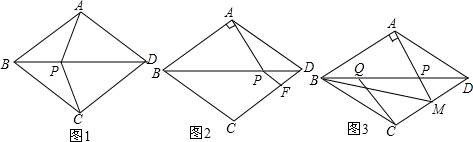    6．如图，△ABD是等腰三角形，AB=AD，将△ABD沿BD翻折得△CBD，点P是线段BD上一点，
    （1）如图1，连接PA、PC，求证：CP=AP；
    （2）如图2，连接PA，若∠BAP=90°时，作∠DPF=45°，线段PF交线段CD于F，求证：AD=AP+DF；
    （3）如图3，∠ABD=30°，连接AP并延长交CD于M，若∠BAM=90°，在BD上取一点Q，且DQ=3BQ，连BM、CQ，当BM=$\frac{15}{2}$时，求CQ的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知直线l：y=-2x+2，且点T（t，$\frac{2}{3}$）在直线l上．
    （1）求OT所在直线的解析式；
    （2）求直线l和直线OT与x轴所围成的图形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．一组数据2，0，-2，1，3的平均数是（　　）
    A．0.8B．1C．1.5D．2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

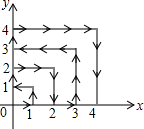    11．如图，一只跳蚤在第一象限及x轴、y轴上跳动，在第一秒钟，它从原点跳动到（1，0），然后接着按图中箭头所示方向跳动，即（0，0）→（0，1）→（1，1）→（0，1）→…，且每秒跳动一个单位，那么第35秒时跳蚤所在位置的坐标是（0，5）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．若一次函数y=-x+b-$\frac{3}{2}$的图象不过第三象限，则b的取值范围是b≥$\frac{3}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．小聪是一名非常爱钻研的七年级学生，他将4块完全一样的三角板（如图1）拼成了一个非常工整的图形（如图2），请教老师以后得知：该图形是一个正方形，并且里面的四边形也是一个正方形．为了作进一步的探究，小明将三角板的三边长用为a，b，c表示（如图3），将两个正方形分别用正方形ABCD和正方形EFGH表示，然后他用两种不同的方法计算了正方形ABCD的面积．
       
    （1）请你用两种不同的方法计算出正方形ABCD面积：
    方法一：方法二：
    （2）根据（1）中计算结果，你能得到怎么样的结论？
    （3）请用文字语言描述（2）中得到的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．如图所示，将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上，若∠1=42°32′，则∠2的度数（　　）
    A．17°28′B．18°28′C．27°28′D．27°32′

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

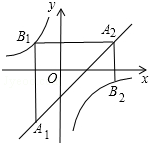    6．如图，已知点A1，A2，…，An均在直线y=x-2上，点B1，B2，…，Bn均在双曲线y=-$\frac{4}{x}$上，并且满足：A1B1⊥x轴，B1A2⊥y轴，A2B2⊥x轴，B2A3⊥y轴，…，AnBn⊥x轴，BnAn+1⊥y轴，…，记点An的横坐标为an（n为正整数）．若a1=-2，则a2016=1．

    查看答案和解析>>

    同步练习册答案