
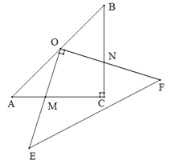
【题目】如图,在Rt△ACB中,AC=BC=8,O为AB的中点,以O为直角顶点作等腰直角三角形OEF,与边AC,BC相交于点M,N.有下列结论:①AM=CN;②CM+CN=8;③![]() ;④当M是AC的中点时,OM=ON.其中正确结论的序号是______.
;④当M是AC的中点时,OM=ON.其中正确结论的序号是______.
【答案】①②④
【解析】
连接OC.由等腰直角三角形的性质得到AO=BO=OC,∠A=∠ACO=∠OCB=45°,OC⊥AO,再由同角的余角相等,得到∠1=∠3,根据ASA即可证明△AMO≌△CNO,根据全等三角形的性质即可得到结论.
连接OC.
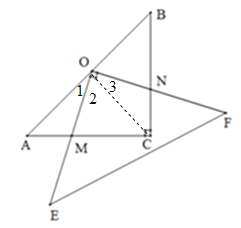
∵Rt△ACB中,AC=BC=8,O为AB的中点,∴AO=BO=OC,∠A=∠ACO=∠OCB=45°,OC⊥AO,∴∠1+∠2=90°.
∵∠EOF=90°,∴∠2+∠3=90°,∴∠1=∠3.
在△AMO和△CNO中,∵∠A=∠OCN=45°,AO=CO,∠1=∠3,∴△AMO≌△CNO,∴AM=CN,故①正确;
∵AM=CN,∴CM+CN=CM+AM=AC=8,故②正确;
∵△AMO≌△CNO,∴S△AMO=S△CNO,∴S四边形OMCN=S△OMC+S△CON= S△OMC+S△AOM=S△AOC=![]() S△ABC=
S△ABC=![]() ×AC×BC=
×AC×BC=![]() ×8×8=16,故③错误;
×8×8=16,故③错误;
∵△AMO≌△CNO,∴MO=NO,故④正确.
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=3,AD=4,动点P从点B出发,以每秒1个单位的速度,沿BA向点A移动;同时点Q从点C出发,以每秒2个单位的速度,沿CB向点B移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤2),解答下列问题:
(1)当x为何值时,PQ⊥DQ;
(2)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最小值?并求出最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 和同一平面内的点
和同一平面内的点![]() .
.
(1)如图1,若点![]() 在
在![]() 边上过点
边上过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 于点
于点![]() .根据题意,请在图1中补全图形,并直接写出
.根据题意,请在图1中补全图形,并直接写出![]() 与
与![]() 的数量关系;
的数量关系;
(2)如图2,若点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,
,![]() .请判断
.请判断![]() 与
与![]() 的位置关系并说明理由;
的位置关系并说明理由;
(3)如图3,点![]() 是
是![]() 外部的一点,过点
外部的一点,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,作
,作![]() 交直线
交直线![]() 于点
于点![]() ,请直接写出
,请直接写出![]() 与
与![]() 的数量关系,并图3中补全图形.
的数量关系,并图3中补全图形.



查看答案和解析>>
科目:初中数学 来源: 题型:
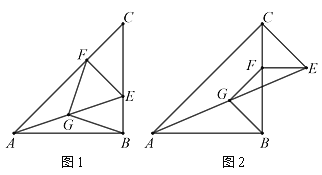
【题目】已知△ABC与△CEF均为等腰直角三角形,∠ABC=∠CFE=90°,连接AE,点G是AE中点,连接BG和GF.
(1)如图1,当△CEF中E、F落在BC、AC边上时,探究FG与BG的关系;
(2)如图2,当△CEF中F落在BC边上时,探究FG与BG的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是ΔABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,BC恰好平分∠ABF,下列结论错误的是( )

A.DE=DFB.AC=3DFC.BD=DCD.AD⊥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红旗镇镇政府大力发动农户扩大柑橘和蔬菜种植面积,取得了较好的经济效益.今年红旗镇柑橘和蔬菜的收成比去年一共增加了80吨,其中柑橘的收成比去年增加了20%,蔬菜的收成比去年增加了30%,从而使今年的收成共达到420吨.
(1)红旗镇去年柑橘和蔬菜的收成各多少吨?
(2)由于今年大丰收,红旗镇政府计划用甲、乙两种货车共33辆将柑橘和蔬菜全部一次性运到外地去销售.已知一辆甲种货车最多可装13吨柑橘和3吨蔬菜;一辆乙种货车最多可装柑橘和蔬菜各6吨,安排甲、乙两种货车共有几种方案?
(3)若甲种货车的运费为每辆600元,乙种货车的运费为每辆500元,在(2)的情况下,如何安排运费最少,最少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
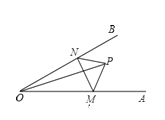
【题目】如图,点P是∠AOB内任意一点,OP=6cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是6cm,则∠AOB的度数是( )
A.25°B.30°
C.60°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知∠A+∠E+∠F+∠C=540°.

(1)试判断直线AB与CD的位置关系,并说明理由;
(2)如图2,∠PAB=3∠PAQ,∠PCD=3∠PCQ,试判断∠APC与∠AQC的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD.求证:EG∥FH.

请完成以下证明过程:
证明:∵AB∥CD(已知)
∴∠AEF=∠EFD(__________________)
∵EG平分∠AEF,FH平分∠EFD(__________)
∴∠___=![]() ∠AEF,∠___=
∠AEF,∠___= ![]() ∠EFD(____________)
∠EFD(____________)
∴∠_____=∠______(等量代换)
∴EG∥FH(__________________).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com