
【题目】如图,一只甲虫在![]() 的方格(每小格边长为1)上沿着网格线运动,他从
的方格(每小格边长为1)上沿着网格线运动,他从![]() 处出发去看望
处出发去看望![]() 、
、![]() 、
、![]() 处的其他甲虫,规定:向上向右走均为正,向下向左走均为负,如果从
处的其他甲虫,规定:向上向右走均为正,向下向左走均为负,如果从![]() 到
到![]() 记为
记为![]() ,从
,从![]() 到
到![]() 记为:
记为:![]() ,其中第一个数表示左右方向,第二个数表示上下方向.
,其中第一个数表示左右方向,第二个数表示上下方向.
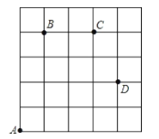
(1)图中![]() {_______,_________},
{_______,_________},![]() {_______,_________};
{_______,_________};
(2)若这只甲虫的行走路线为![]() ,请计算该甲虫走过的最短路程.
,请计算该甲虫走过的最短路程.
(3)若图中另有两个格点![]() 、
、![]() ,且
,且![]() ,
,![]() ,则
,则![]() 应记为什么?直接写出你的答案.
应记为什么?直接写出你的答案.
【答案】(1){3,4 }, {-2,0};(2)10;(3){-2,-2 }.
【解析】
(1)根据向上向右走均为正,向下向左走均为负分别写出各点的坐标即可;图中A→C{ 3,4},C→B{-2,0};
(2)分别根据各点的坐标计算总长即可;
(3)令M→A与M→N对应的横纵坐标相减即可得出.
解:(1)∵规定:向上向右走均为正,向下向左走均为负,
∴图中![]() {3,4 },
{3,4 },![]() {-2,0};
{-2,0};
(2)根据已知条件可知:
![]() 表示为:{1,4 },
表示为:{1,4 },![]() 记为{2,0 },
记为{2,0 },![]() 记为{1,-2 };
记为{1,-2 };
则该甲虫走过的路线长为:![]() ;
;
(3)由![]() ,
,![]() ,
,
所以,5-a-(3-a)=2,b-2-(b-4)=2, 所以,点A向右走2个格点,向上走2个格点到点N,
所以,N→A应记为{-2,-2 }.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校为了分析九年级学生艺术考试的成绩,随机抽查了两个班的各5名学生的成绩,它们分别为:
九(1)班 :96,92,94,97,96;
九(2)班 :90,98,97,98,92.
通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 |
九(1)班 | 95 | a | 96 |
九(2)班 | 95 | 97 | b |
(1)a= , b = ;
(2)计算两个班所抽取的学生艺术成绩的方差,判断哪个班学生的艺术成绩比较稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(3,﹣6)是二次函数y=ax2上的一点,则这二次函数的解析式是 .
【答案】y=﹣![]() x2
x2
【解析】
试题分析:将点A(3,﹣6)代入y=ax2,利用待定系数法法求该二次函数的解析式即可得﹣6=9a,
解得a=﹣![]() ;因此该二次函数的解析式为:y=﹣
;因此该二次函数的解析式为:y=﹣![]() x2.
x2.
考点:待定系数法求二次函数解析式
【题型】填空题
【结束】
15
【题目】在一个不透明的口袋中装有8个红球和若干个白球,它们除颜色外其它完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在40%附近,则口袋中白球可能有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
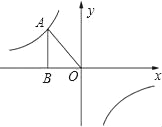
【题目】如图,已知反比例函数y=![]() (k≠0)的图象经过点A(﹣2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.
(k≠0)的图象经过点A(﹣2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.
(Ⅰ)求k和m的值;
(Ⅱ)设C(x,y)是该反比例函数图象上一点,当1≤x≤4时,求函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=∠BFD.
(1)求证:FD是⊙O的一条切线;
(2)若AB=10,AC=8,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,已知数
,已知数![]() 是最小的正整数,且
是最小的正整数,且![]() 、
、![]() 满足
满足![]() .
.
![]()
(1)![]() ,
,![]() ,
,![]() ;
;
(2)若将数轴折叠,使得点![]() 与点
与点![]() 重合,则点
重合,则点![]() 与数 表示的点重合;
与数 表示的点重合;
(3)点![]() 、
、![]() 、
、![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒1个单位长度的速度向左运动,同时,点
以每秒1个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒2个单位长度和4个单位长度的速度向右运动,假设
分别以每秒2个单位长度和4个单位长度的速度向右运动,假设![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,求
,求![]() 、
、![]() 、
、![]() 的长(用含
的长(用含![]() 的式子表示);
的式子表示);
(4)在(3)的条件下,![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若改变,请说明理由;若不变,请求其值.
的变化而改变?若改变,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动.如图折线OAB和线段CD分别表示小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象.根据图中提供的信息,解答下列问题:
(1)小帅的骑车速度为 千米/小时;点C的坐标为 ;
(2)求线段AB对应的函数表达式;
(3)当小帅到达乙地时,小泽距乙地还有多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D为AB边上一点,E为CD中点,AC=![]() ,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )
,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )

A. ![]() B.
B. ![]() +1﹣
+1﹣![]() C.
C. ![]() ﹣
﹣![]() D.
D. ![]() ﹣1
﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com