
分析 (1)根据全等三角形对应边相等解答;
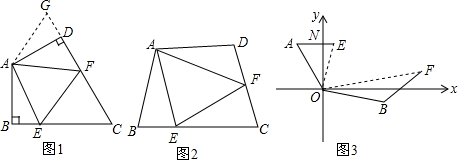
(2)延长FD到G,使DG=BE,连接AG,根据同角的补角相等求出∠B=∠ADG,然后利用“边角边”证明△ABE和△ADG全等,根据全等三角形对应边相等可得AE=AG,∠BAE=∠DAG,再求出∠EAF=∠GAF,然后利用“边角边”证明△AEF和△GAF全等,根据全等三角形对应边相等可得EF=GF,然后求解即可;
(3)连接EF,延长AE、BF相交于点C,然后求出∠EAF=$\frac{1}{2}$∠AOB,判断出符合探索延伸的条件,再根据探索延伸的结论解答即可.
解答 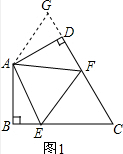 解:(1)EF=BE+DF;
解:(1)EF=BE+DF;
证明:如图1,延长FD到G,使DG=BE,连接AG,
在△ABE和△ADG中,
$\left\{\begin{array}{l}{DG=BE}\\{∠B=∠ADG}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
$\left\{\begin{array}{l}{AE=AG}\\{∠EAF=∠GAF}\\{AF=AF}\end{array}\right.$,
∴△AEF≌△GAF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
故答案为:EF=BE+DF;
(2)EF=BE+DF仍然成立. 证明:如图2,延长FD到G,使DG=BE,连接AG,
证明:如图2,延长FD到G,使DG=BE,连接AG,
∵∠B+∠ADC=180°,∠ADC+∠ADG=180°,
∴∠B=∠ADG,
在△ABE和△ADG中,
$\left\{\begin{array}{l}{DG=BE}\\{∠B=∠ADG}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=$\frac{1}{2}$∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
$\left\{\begin{array}{l}{AE=AG}\\{∠EAF=∠GAF}\\{AF=AF}\end{array}\right.$,
∴△AEF≌△GAF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
(3)如图3,连接EF,延长AE、BF相交于点C,
∵∠AOB=20°+90°+(90°-60°)=140°,
∠EOF=70°,
∴∠EOF=$\frac{1}{2}$∠AOB,
又∵OA=OB,
∠OAC+∠OBC=(90°-20°)+(60°+50°)=180°,
∴符合探索延伸中的条件,
∴结论EF=AE+BF成立,
即EF=583米.
点评 本题考查了全等三角形的判定与性质,读懂问题背景的求解思路,作辅助线构造出全等三角形并两次证明三角形全等是解题的关键,也是本题的难点.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
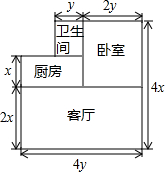 (1)一家住房的结构如图所示,这家房子的主人打算把卧室以外的部分都铺上地砖,至少需要多少m2的地砖?如果每1m2地砖的价格是a元钱,则购买所需地砖至少需要多少元?
(1)一家住房的结构如图所示,这家房子的主人打算把卧室以外的部分都铺上地砖,至少需要多少m2的地砖?如果每1m2地砖的价格是a元钱,则购买所需地砖至少需要多少元?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图.正比例函数y=kx与反比例函数y=$\frac{m}{x}$的图象相交于A(1,a)、C(b,-1)两点,过A作x轴的垂线交x轴于B,连BC.
如图.正比例函数y=kx与反比例函数y=$\frac{m}{x}$的图象相交于A(1,a)、C(b,-1)两点,过A作x轴的垂线交x轴于B,连BC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD、DEFH的边长都是5cm,点P从点D出发,先到点A,然后沿箭头所指方向运动(经过点D时不拐弯),则从出发开始连续运动2014cm时,它离点C 最近,此时它距该点1cm.
如图,正方形ABCD、DEFH的边长都是5cm,点P从点D出发,先到点A,然后沿箭头所指方向运动(经过点D时不拐弯),则从出发开始连续运动2014cm时,它离点C 最近,此时它距该点1cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com