
【题目】如图,点E在线段CD上,EA、EB分别平分∠DAB和∠CBA,点F在线段AB上运动,AD=4cm,BC=3cm,且AD∥BC.
(1)你认为AE和BE有什么位置关系?并验证你的结论;
(2)当点F运动到离点A多少厘米时,△ADE和△AFE全等?为什么?
(3)在(2)的情况下,此时BF=BC吗?证明你的结论并求出AB的长.
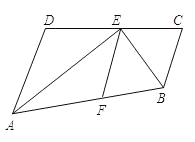
【答案】(1)AE⊥BE;(2)当点F运动到离点A为4cm(即AF=AD=4cm)时,△ADE≌△AFE;(3)BF=BC;AB=7cm
【解析】试题分析:(1)、首先根据角平分线的性质得出∠EAB+∠EBA=![]() (∠DAB+∠ABC),根据平行线的性质可以得出∠EAB+∠EBA=90°,从而得出答案;(2)、要使得△ADE和△AFE全等,则必须满足AF=AD,则AF=AD=4cm;(3)、首先根据△AFE和△ADE全等得出∠D=∠AFE,然后根据平行线的性质以及平角的性质得出∠C=∠BFE,然后结合角平分线和公共边得出三角形全等,然后得出BF=BC=3cm,从而求出AB的长度.
(∠DAB+∠ABC),根据平行线的性质可以得出∠EAB+∠EBA=90°,从而得出答案;(2)、要使得△ADE和△AFE全等,则必须满足AF=AD,则AF=AD=4cm;(3)、首先根据△AFE和△ADE全等得出∠D=∠AFE,然后根据平行线的性质以及平角的性质得出∠C=∠BFE,然后结合角平分线和公共边得出三角形全等,然后得出BF=BC=3cm,从而求出AB的长度.
试题解析:(1)、AE⊥BE; ∵EA、EB分别平分∠DAB和∠CBA,∴∠2=![]() ∠DAB,∠3=
∠DAB,∠3=![]() ∠ABC,∵AD∥BC,∴∠DAB+∠ABC=180°,∴∠2+∠3=90°,∴∠AEB=90°,∴AE⊥BE;
∠ABC,∵AD∥BC,∴∠DAB+∠ABC=180°,∴∠2+∠3=90°,∴∠AEB=90°,∴AE⊥BE;
(2)、当点F运动到离点A为4cm(即AF=AD=4cm)时,△ADE≌△AFE;
∵EA、EB分别平分∠DAB和∠CBA,∴∠1=∠2,∠3=∠4,在△AFE与△ADE中有∠1=∠2,AE=AE,AF=AD,∴△AFE≌△ADE;
(3)、BF=BC;∵△AFE≌△ADE,∴∠D=∠5,∵AD∥BC,∴∠D+∠C=180°,∵∠5+∠6=180°,∴∠C=∠6,
在△ECB与△EFB中有∠3=∠4 ∠C=∠6 BE=BE`
∴△ECB≌△EFB,∴BF=BC. ∵AF=AD=4cm,BF=BC=3cm,
∴AB=AF+BF=3+4=7(cm).


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
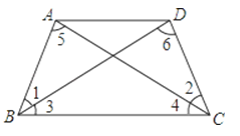
【题目】如图,已知∠3=∠4,要说明△ABC≌△DCB,
(1)若以“SAS”为依据,则需添加一个条件是________
(2)若以“AAS”为依据,则需添加一个条件是________
(3)若以“ASA”为依据,则需添加一个条件是________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各式,且把结果化为只含有正整数指数的形式:
(1)(x﹣2)﹣3(yz﹣1)3 ;(2)a2b3(2a﹣1b)3
(3)(3a3b2c﹣1)﹣2(5ab﹣2c3)2;(4)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
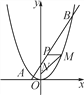
【题目】如图,已知一条直线过点(0,4),且与抛物线y=![]() x2交于A,B两点,其中点A的横坐标是-2.
x2交于A,B两点,其中点A的横坐标是-2.
(1)求这条直线的解析式及点B的坐标;
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有1个,若从中随机摸出一个球,这个球是白球的概率为![]() .
.
(1)求袋子中白球的个数;(请通过列式或列方程解答)
(2)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形ABC中,∠C=90°,点O为AB上的一点,以点O为圆心,OA为半径的圆弧与BC相切于点D,交AC于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)已知AE=2,DC=![]() ,求圆弧的半径.
,求圆弧的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新学期开学,某体育用品商店开展促销活动,有两种优惠方案.
方案一:不购买会员卡时,乒乓球享受8.5折优惠,乒乓球拍购买5副(含5副)以上才能享受8.5折优惠,5副以下必须按标价购买.
方案二:办理会员卡时,全部商品享受八折优惠,小健和小康的谈话内容如下:

会员卡只限本人使用.
(1)求该商店销售的乒乓球拍每副的标价.
(2)如果乒乓球每盒10元,小健需购买乒乓球拍6副,乒乓球a盒,请回答下列问题:
①如果方案一与方案二所付钱数一样多,求a的值;
②直接写出一个恰当的a值,使方案一比方案二优惠;
③直接写出一个恰当的a值,使方案二比方案一优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简下列多项式:
(1)![]()
(2)![]()
(3)若![]() ,求
,求![]() 的值.
的值.
(4)先化简,再求值:(2x﹣1)2﹣(3x+1)(3x﹣1)+5x(x﹣1),其中x=﹣2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 (1),已知△ABC是等边三角形,以BC为直径的⊙O交AB、AC于D、E.求证:

(1)△DOE是等边三角形.
(2)如图(2),若∠A=60°,AB≠AC, 则(1)中结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com