解:(1)y=ax
2-2ax+b=a(x-1)
2-a+b,
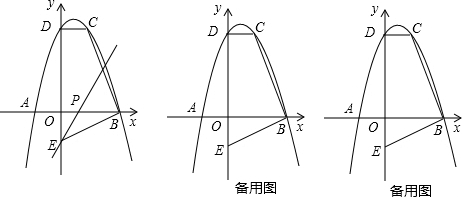
∵过点A(-2,0),C(2,8),
∴
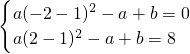
解得
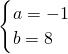
.
故此抛物线的解析式为y=-x
2+2x+8;
(2)由抛物线的解析式为y=-x
2+2x+8可得B(4,0),
∵P(4-t,0),E(0,-2),
设一次函数EP的解析式为y=kx+b,将P(4-t,0),E(0,-2)分别代入解析式得,

,
解得,
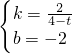
,
一次函数解析式为y=

x-2.
设BC的解析式为y=ax+c,
将C(2,8),B(4,0)代入解析式得,

,
解得
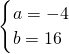
,
函数解析式为y=-4x+16.
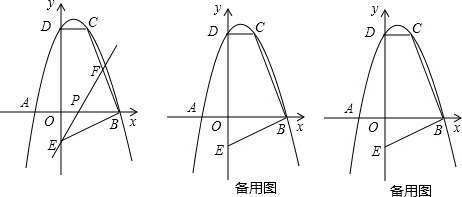
将y=-4x+16和y=

x-2组成方程组得,
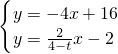
,
解得

,
S=

×(4-t)×

=

.
(3)分为3种情况,①旋转后OE在抛物线上;②旋转后OB在抛物线上;③旋转后BE在抛物线上.
1、旋转后OE在抛物线上:
设为O′E′,则O′E′平行于x轴,抛物线y=-x
2+2x+8=-(x-1)
2+9,对称轴x=1,
则x
1=1-

|OE|=1-1=0,x
2=1+1=2.
则两点为(0,8)、(2,8).
这时分别:①O′(0,8)、E′(2,8);
②E′(0,8)、O′(2,8).
然后分两种情况分别作OO',EE'的中垂线,其交点即为其旋转中心.
∵OO′的解析式为y=4,易得,EE′的解析式为y=5x-2,则EE′的中点坐标为(1,3),
其中垂线解析式为y=-

x+b,将(1,3)代入解析式得,b=
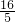
,
则解析式为y=-

x+
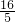
,当y=4时,x=-4.
旋转中心坐标为(-4,4).
2、旋转后OB在抛物线上:
OB∥y轴,则O′B′∥x轴,但抛物线y=-x
2+2x+8=-(x-1)
2+9,不成立.
3、旋转后BE在抛物线上:
BE边旋转90°后所得线段B'E'与BE垂直,直线斜率k
BE=

,则k
B'E'=-2.
设旋转后B'E'所在直线方程为:y=-2x+m.
抛物线:y=-x
2+2x+8,联立,解方程,得:
(x,y)=(2+

,m-4-2

) 或 (x,y)=(2-

,m-4+2

)
此为两交点坐标,求距离使其等于|BE|=
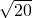
=2

.有:
|BE|=

=
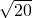
,从而有m=11,
两点坐标:(3,5),(1,9).
然后分1)B′(3,5),E′(1,9);2)E′(3,5),B′(1,9)两种情况,
分别作BB′与EE′的垂直平分线,两者交点即为其旋转中心.
综上,同1中解法,共有4种可能性,4个旋转中心,(-4,4)(5,3)(6,3)(-2,3).
分析:(1)将原式配方,再将A(-2,0),C(2,8)代入解析式即可求出a、b的值,从而得到函数的解析式;
(2)将扫过的面积转化为△PEB和△PFB两个三角形的面积之和来表示,用含t的代数式表示出BP的长,表示出P点坐标,求出直线PE的表达式,再求出直线BC的解析式,将二者组成方程组,求出F的纵坐标,即可表示出△PFB的面积表达式;易得,△BPE的表达式,将二者相加即可.
(3)分为3种情况,①旋转后OE在抛物线上;②旋转后OB在抛物线上;③旋转后BE在抛物线上解答.
点评:本题考查了二次函数的综合运用,涉及待定系数法求一次函数解析式,抛物线的性质、方程组的解法等知识,综合性极强,难度较大.

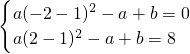
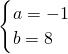 .
. ,
,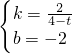 ,
, x-2.
x-2. ,
,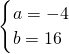 ,
, x-2组成方程组得,
x-2组成方程组得,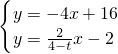 ,
, ,
, ×(4-t)×
×(4-t)× =
= .
.
 |OE|=1-1=0,x2=1+1=2.
|OE|=1-1=0,x2=1+1=2. x+b,将(1,3)代入解析式得,b=
x+b,将(1,3)代入解析式得,b=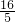 ,
, x+
x+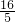 ,当y=4时,x=-4.
,当y=4时,x=-4. ,则kB'E'=-2.
,则kB'E'=-2. ,m-4-2
,m-4-2 ) 或 (x,y)=(2-
) 或 (x,y)=(2- ,m-4+2
,m-4+2 )
)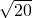 =2
=2 .有:
.有: =
=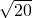 ,从而有m=11,
,从而有m=11,

 名校课堂系列答案
名校课堂系列答案 =2
=2
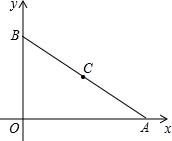 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.