(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵∠ACB=∠E+∠CBE,
∴∠ABC=∠E+∠CBE,
∴∠ABE=∠ABC+∠CBE=2∠CBE+∠BEC=90°,
∵AB为⊙O直径,
∴BE是⊙O的切线;
(2)解:设AE于圆交于点M,连接BM,过点C作CF⊥BE于F,
∵AB为⊙O直径,
∴∠AMB=90°,
∴∠MBE+∠BEC=90°,
∵∠BEC+2∠CBE=90°,
∴∠MBE=2∠CBE,
∴∠MBC=∠FBC,
∴△MBC≌△FBC,
∵tan∠CBE=

,
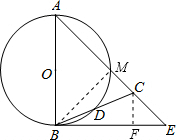
∴设CF=1,则BF=2,
∴BM=BF=2,CM=CF=1,
再设AM=x,
在Rt△AMB中,
AM=x,AB=AC=1+x,BM=2,
∴x
2+2
2=(x+1)
2,
解得:x=

,
∴AB=

,
∵∠A+∠MBA=90°,∠A+∠E=90°,
∴∠E=∠MBA,
∴sin∠E=sin∠MBA=
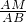
=
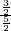
=

.
分析:(1)根据等腰三角形的性质和三角形的外角和定理以及已知条件即可证明∠ABE=90°,进而证明BE是⊙O的切线;
(2)设AE于圆交于点M,连接BM,过点C作CF⊥BE于F,利用圆周角定理以及全等三角形的性质和勾股定理即可求出AG的长,进而求出圆的直径,sin∠E的值也可求出.
点评:本题考查了圆的切线的判定定理、三角形的外角和定理、等腰三角形的性质、全等三角形的判定和性质、勾股定理的运用以及锐角三角函数的运用,题目的综合性很强,难度不小,解题的关键是作垂线段构造全等三角形.

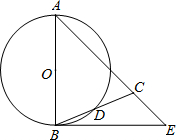 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,E是AC的延长线上一点,连接BE,∠BEC+2∠CBE=90°.
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,E是AC的延长线上一点,连接BE,∠BEC+2∠CBE=90°. ,求sin∠E的值.
,求sin∠E的值. ,
,
 ,
, ,
,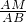 =
=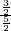 =
= .
.

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.