
【题目】为从小明和小刚中选出一人去观看元旦文艺汇演,现设计了如下游戏,规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏是否公平.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校初二数学兴趣小组活动时,碰到这样一道题:
“已知正方形AD,点E、F、G、H分别在边AB、BC、CD、DA上,若![]() ,则EG=FH”.
,则EG=FH”.
经过思考,大家给出了以下两个方案:
(甲)过点A作AM∥HF交BC于点M,过点B作BN∥EG交CD于点N;
(乙)过点A作AM∥HF交BC于点M,作AN∥EG交CD的延长线于点N;
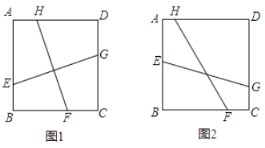
(1)对小杰遇到的问题,请在甲、乙两个方案中任选一个,加以证明(如图1)
(2)如果把条件中的“![]() ”改为“EG与FH的夹角为45°”,并假设正方形ABCD的边长为1,FH的长为
”改为“EG与FH的夹角为45°”,并假设正方形ABCD的边长为1,FH的长为![]() (如图2),试求EG的长度.
(如图2),试求EG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
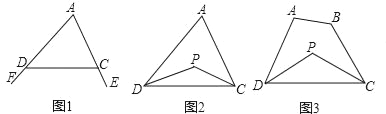
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠BAC=90°,分别以 AC 和 BC 为边向外作正方形 ACFG 和正方形 BCDE,过点 D 做 FC 的延长线的垂线,垂足为点 H.
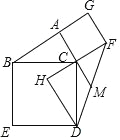
(1)求证:△ABC≌△HDC;
(2)连接 FD,交 AC 的延长线于点 M,若 AG=![]() ,tan∠ABC=
,tan∠ABC= ![]() ,求△FCM 的面积.
,求△FCM 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,(1)数轴上的所有点都表示有理数;(2)无理数可以用数轴上的点表示;(3)实数与数轴上的点一一对应;(4)无限小数是无理数;(5)带根号的数都是无理数;(6)数轴上的点不是表示有理数,就是表示无理数;错误命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
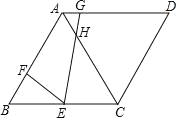
【题目】如图,在菱形ABCD中,∠B=60°,BC=6,E为BC中点,F是AB上一点,G为AD上一点,且BF=2,∠FEG=60°,EG交AC于点H,下列结论:①△BEF∽△CHE;②AG=1;③EH=![]() ;④S△BEF=3S△AGH;正确的是______.(填序号即可)
;④S△BEF=3S△AGH;正确的是______.(填序号即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践 问题情境:
综合与实践课上,同学们以“三角形纸片的折叠与旋转“为主题展开数学活动,探究有关的数学问题.
动手操作:
已知:三角形纸片![]() 中,
中,![]() .将三角形纸片
.将三角形纸片![]() 按如下步骤进行操作:
按如下步骤进行操作:
第一步:如图1,折叠三角形纸片![]() ,使点
,使点![]() 与点
与点![]() 重合,然后展开铺平,折痕分别交
重合,然后展开铺平,折痕分别交![]() 于点
于点![]() ,连接
,连接![]() ,易知
,易知![]() .
.
第二步:在图1的基础上,将三角形纸片![]() 沿
沿![]() 剪开,得到
剪开,得到![]() 和
和![]() .保持
.保持![]() 的位置不变,将
的位置不变,将![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() (点
(点![]() 分别是
分别是![]() 的对应点),旋转角为
的对应点),旋转角为![]() 问题解决:
问题解决:
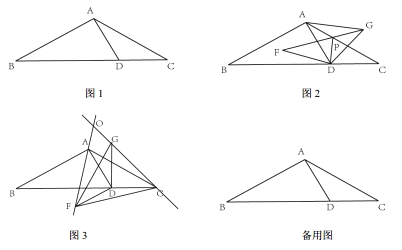
(1)如图2,小彬画出了旋转角![]() 时的图形,设线段
时的图形,设线段![]() 交于点
交于点![]() ,连接
,连接![]() .小彬发现
.小彬发现![]() 所在直线始终垂直平分线段
所在直线始终垂直平分线段![]() .请证明这一结论;
.请证明这一结论;
(2)如图3,小颖画出了旋转角![]() 时的图形,设直线
时的图形,设直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,连接
,连接![]() 判断此时
判断此时![]() 的形状,说明理由;
的形状,说明理由;
(3)在![]() 绕点
绕点![]() 逆时针旋转过程中,当
逆时针旋转过程中,当![]() 时,请直接写出
时,请直接写出![]() 两点间的距离.
两点间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com