
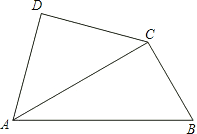
【题目】将一副三角尺如图拼接:含![]() 角的三角尺
角的三角尺![]() 的长直角边与含
的长直角边与含![]() 角的三角尺
角的三角尺![]() 的斜边恰好重合
的斜边恰好重合![]() 已知
已知![]() 是AC上的一个动点.
是AC上的一个动点.
![]() 当点P运动到
当点P运动到![]() 的平分线上时,连接DP,求DP的长;
的平分线上时,连接DP,求DP的长;
![]() 当点P在运动过程中出现
当点P在运动过程中出现![]() 时,求此时
时,求此时![]() 的度数;
的度数;
![]() 当点P运动到什么位置时,以
当点P运动到什么位置时,以![]() 为顶点的平行四边形的顶点Q恰好在边BC上?求出此时DPBQ的面积.
为顶点的平行四边形的顶点Q恰好在边BC上?求出此时DPBQ的面积.
【答案】(1)![]() ;(2)
;(2)![]() 的度数为
的度数为![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)、作DF⊥AC,由AB的长求得BC、AC的长.在等腰Rt△DAC中,DF=FA=FC;在Rt△BCP中,求得PC的长.则由勾股定理即可求得DP的长;(2)、由(1)得BC与DF的关系,则DP与DF的关系也已知,先求得∠PDF的度数,则∠PDA的度数也可求出,需注意有两种情况;(3)、由于四边形DPBQ为平行四边形,则BC∥DF,P为AC中点,作出平行四边形,求得面积.
详解:(1)解:在![]() 中,
中,![]() ,
,
![]() .
.
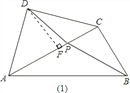
![]() 如图
如图![]() ,作
,作![]() .
.
![]() 中,
中,![]() ,
,![]() .
.![]() 平分
平分![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
![]() 当P点位置如图
当P点位置如图![]() 所示时,根据
所示时,根据![]() 中结论,
中结论,![]() ,
,
又![]() ,
,![]() ,
,![]() .
.
![]() .
.
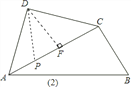
当P点位置如图![]() 所示时,同
所示时,同![]() 可得
可得![]() .
.
![]() . 故
. 故![]() 的度数为
的度数为![]() 或
或![]() ;
;
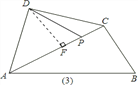
![]() 当点P运动到边AC中点
当点P运动到边AC中点![]() 如图
如图![]() ,即
,即![]() 时,
时,
以![]() 为顶点的平行四边形的顶点Q恰好在边BC上.
为顶点的平行四边形的顶点Q恰好在边BC上.
![]() 四边形DPBQ为平行四边形,
四边形DPBQ为平行四边形,![]() ,
,![]() ,
,![]() ,即
,即![]() .
.
而在![]() 中,
中,![]() ,
,![]() 根据勾股定理得:
根据勾股定理得:![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() ,
,
![]() 是平行四边形DPBQ的高,
是平行四边形DPBQ的高,![]() .
.



 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】(1)先观察下列等式,再完成题后问题:
![]() ,
,![]() ,
,![]()
①请你猜想:![]() =________.
=________.
②若a、b为有理数,且![]() ,
,
求:![]() +…+
+…+![]() 的值.
的值.
(2)探究并计算:![]() +
+![]() +
+![]() +…+
+…+![]()
(3)如图,把一个面积为1的正方形等分成两个面积为![]() 的长方形,接着把面积为
的长方形,接着把面积为![]() 的长方形等分成两个面积为
的长方形等分成两个面积为![]() 的正方形,再把面积为
的正方形,再把面积为![]() 的正方形等分成两个面积为
的正方形等分成两个面积为![]() 的矩形.如此进行下去,试利用图形揭示的规律计算:
的矩形.如此进行下去,试利用图形揭示的规律计算:![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() .(直接写答案).
.(直接写答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形。若![]() ,AB=2,则图中阴影部分的面积为______.
,AB=2,则图中阴影部分的面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2-2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象.如图,当直线y=-x+n与此图象有且只有两个公共点时,则n的取值范围为 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1 , x2 .
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 与
与![]() 成正比例,且
成正比例,且![]() 时,
时,![]() .
.
(1)求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)在所给的直角坐标系(如图)中画出函数的图象;
(3)直接写出当![]() 时,自变量
时,自变量![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发门市销售两种商品,甲种商品每件售价为300元,乙种商品每件售价为80元.新年来临之际,该门市为促销制定了两种优惠方案:
方案一:买一件甲种商品就赠送一件乙种商品;
方案二:按购买金额打八折付款.
某公司为奖励员工,购买了甲种商品20件,乙种商品x(x≥20)件.
(1)分别写出优惠方案一购买费用y1(元)、优惠方案二购买费用y2(元)与所买乙种商品x(件)之间的函数关系式;
(2)若该公司共需要甲种商品20件,乙种商品40件.设按照方案一的优惠办法购买了m件甲种商品,其余按方案二的优惠办法购买.请你写出总费用w与m之间的关系式;利用w与m之间的关系式说明怎样购买最实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元. ①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com