
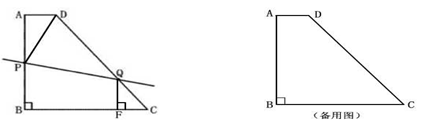
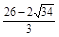 ��8��t��10��10��t��12ʱ����P��D��QΪ�����������ǡ������DQΪһ���ĵ���������
��8��t��10��10��t��12ʱ����P��D��QΪ�����������ǡ������DQΪһ���ĵ���������
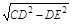 =
=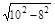 ="6"
="6" 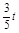 ��QF=
��QF=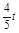 ����PG=
����PG=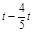 =
=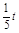 ��QG=8��
��QG=8��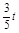
 =��8��t��2+22=t2��16t+68��
=��8��t��2+22=t2��16t+68��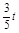 ��2+��
��2+��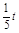 ��2=
��2=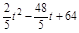
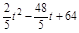 ��
�� 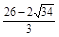 ��t2=
��t2= ��8����ȥ������ʱt=
��8����ȥ������ʱt=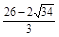 ��������6��
��������6��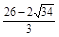 ��8��t��10��10��t��12ʱ����P��D��QΪ�����������ǡ������DQΪһ���ĵ���������. ������������������10��
��8��t��10��10��t��12ʱ����P��D��QΪ�����������ǡ������DQΪһ���ĵ���������. ������������������10��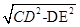 ���CE���������BC�ij����Ӷ��������ABCD���ܳ�
���CE���������BC�ij����Ӷ��������ABCD���ܳ� ������CF=
������CF= 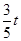 ��QF=
��QF=  ������PG=t
������PG=t =
=  ��QG=8-
��QG=8-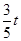 ��Ȼ��ֱ���t��ʾ��PD2=t2-16t+68��PQ2=
��Ȼ��ֱ���t��ʾ��PD2=t2-16t+68��PQ2=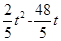 +64����DQ=PD����10-t��2=t2-16t+68����DQ=PQ����10-t��2=
+64����DQ=PD����10-t��2=t2-16t+68����DQ=PQ����10-t��2=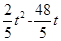 +64�����ⷽ�̼��ɣ�
+64�����ⷽ�̼��ɣ�


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 S�ı���OQPBʱ����ȷ����P��AB�ϵ�λ�ã�������߶�PQ�ij���
S�ı���OQPBʱ����ȷ����P��AB�ϵ�λ�ã�������߶�PQ�ij���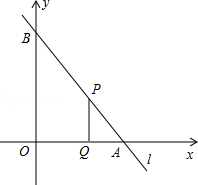
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
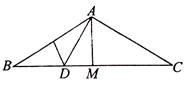
| A��1�� | B��2�� | C��3�� | D��4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
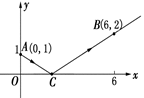
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

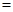 3��AC=3
3��AC=3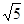 �����O�İ뾶����
�����O�İ뾶�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
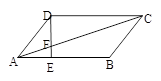
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com