
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,其中
两点,其中![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线的对称轴交
,抛物线的对称轴交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() ,连接
,连接![]() .
.
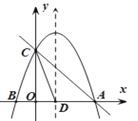
(1)求抛物线和直线![]() 的解析式:
的解析式:
(2)若抛物线上存在一点![]() ,使
,使![]() 的面积是
的面积是![]() 面积的2倍,求点
面积的2倍,求点![]() 的坐标;
的坐标;
(3)在抛物线的对称轴上是否存在一点![]() ,使线段
,使线段![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 得到线段
得到线段![]() ,且
,且![]() 恰好落在抛物线上?若存在,求出点
恰好落在抛物线上?若存在,求出点![]() 的坐标;若不存在,请说叫理由.
的坐标;若不存在,请说叫理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)存在,点
;(3)存在,点![]() 的坐标为
的坐标为![]() 和
和![]() .
.
【解析】
(1)先利用待定系数法求出抛物线的解析式,从而可求出点C的坐标,再利用待定系数法即可求出直线AC的解析式;
(2)先根据二次函数的性质可得![]() ,从而可得
,从而可得![]() ,再根据平行线的性质可知过点B作
,再根据平行线的性质可知过点B作![]() ,与抛物线的交点即为其他符合条件的点P,然后联立直线BE和抛物线的解析式求解即可得;
,与抛物线的交点即为其他符合条件的点P,然后联立直线BE和抛物线的解析式求解即可得;
(3)分当点Q在x轴的上方和当点Q在x轴的下方两种情况,再分别根据直角三角形的性质、三角形全等的判定定理与性质、二次函数的性质求解即可得.
(1)把![]() ,
,![]() 代入
代入![]() 得
得![]()
解得![]()
∴抛物线的解析式为![]()
当![]() 时,
时,![]()
∴点![]() 的坐标是
的坐标是![]()
把![]() ,
,![]() 代入
代入![]() 得
得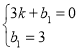
解得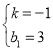
∴直线![]() 的解析式为
的解析式为![]() ;
;
(2)∵![]()
∴![]()
如图,过![]() 点作
点作![]()
由平行线的性质可知,直线BE上的点到AC的距离均相等
则直线BE上的任意一点与点A、C组成的三角形的面积均等于![]() 的面积,均为
的面积,均为![]() 面积的2倍
面积的2倍
![]()
![]() 设直线BE的解析式为
设直线BE的解析式为![]()
将点![]() 代入得
代入得![]() ,解得
,解得![]()
则直线BE的解析式为![]()
联立![]() ,解得
,解得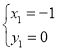 ,
,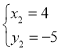
故符合条件的点![]() 的坐标为
的坐标为![]() ,
,![]() ;
;
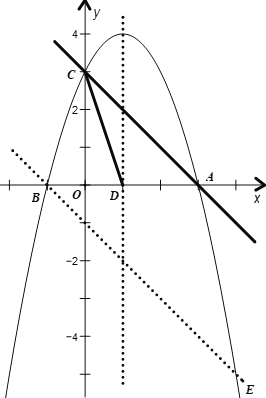
(3)由题意,分以下两种情况:
①当点Q在x轴的上方
设![]() 与对称轴交点为
与对称轴交点为![]()
由![]() 可知,抛物线的对称轴为
可知,抛物线的对称轴为![]()
令![]() 代入
代入![]() 得
得![]()
∴![]() 坐标为
坐标为![]()
∴![]()
∴![]()
∴![]()
∴![]() 即为所求
即为所求
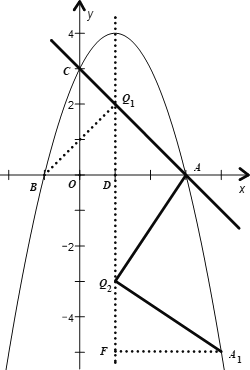
②当点Q在x轴的下方
如图,过点![]() 作
作![]() 于点F
于点F
![]()
![]()
![]()
由旋转的性质得:![]()
在![]() 和
和![]() 中,
中,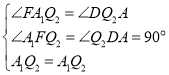
![]()
![]()
设![]() ,则
,则![]()
![]() 点
点![]() 的横坐标为
的横坐标为![]() ,纵坐标为
,纵坐标为![]() ,即
,即![]()
将![]() 代入
代入![]() 得
得![]()
解得![]() 或
或![]() (不符题意,舍去)
(不符题意,舍去)
即![]()
![]() 的坐标为
的坐标为![]()
综上,点![]() 的坐标为
的坐标为![]() 和
和![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,在正方形![]() 中,
中,![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,连接
运动,连接![]() 交
交![]() 于
于![]() 连接
连接![]() .
.
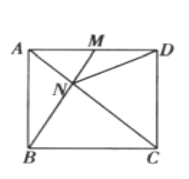
(1)证明:无论![]() 运动到
运动到![]() 上的何处,都有
上的何处,都有![]() ;
;
(2)当![]() 运动到何处时,
运动到何处时,![]() ?
?
(3)若![]() 从
从![]() 到
到![]() 再从
再从![]() 到
到![]() ,在整个运动过程中,
,在整个运动过程中,![]() 为多少时,
为多少时,![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,![]() ),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值_____.
),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】游乐园新建的一种新型水上滑道如图,其中线段![]() 表示距离水面(x轴)高度为5m的平台(点P在y轴上).滑道
表示距离水面(x轴)高度为5m的平台(点P在y轴上).滑道![]() 可以看作反比例函数图象的一部分,滑道
可以看作反比例函数图象的一部分,滑道![]() 可以看作是二次函数图象的一部分,两滑道的连接点B为二次函数
可以看作是二次函数图象的一部分,两滑道的连接点B为二次函数![]() 的顶点,且点B到水面的距离
的顶点,且点B到水面的距离![]() ,点B到y轴的距离是5m.当小明从上而下滑到点C时,与水面的距离
,点B到y轴的距离是5m.当小明从上而下滑到点C时,与水面的距离![]() ,与点B的水平距离
,与点B的水平距离![]() .
.
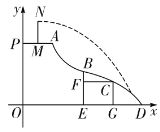
(1)求反比例函数的关系式及其自变量的取值范围;
(2)求整条滑道![]() 的水平距离;
的水平距离;
(3)若小明站在平台上相距y轴![]() 的点M处,用水枪朝正前方向下“扫射”,水枪出水口N距离平台
的点M处,用水枪朝正前方向下“扫射”,水枪出水口N距离平台![]() ,喷出的水流成抛物线形,设这条抛物线的二次项系数为p,若水流最终落在滑道
,喷出的水流成抛物线形,设这条抛物线的二次项系数为p,若水流最终落在滑道![]() 上(包括B、D两点),直接写出p的取值范围.
上(包括B、D两点),直接写出p的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ,
,![]() ,
,![]() .
.
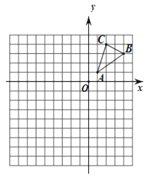
(1)请作出![]() 绕
绕![]() 点逆时针旋转
点逆时针旋转![]() 的
的![]() ;
;
(2)以点![]() 为位似中心,将
为位似中心,将![]() 扩大为原来的2倍,得到
扩大为原来的2倍,得到![]() ,请在
,请在![]() 轴的左侧画出
轴的左侧画出![]() ;
;
(3)请直接写出![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华优秀传统文化,某校组织了“古诗词”知识竞赛,由九年级的若干名学生参加选拔赛,从中选出10名优胜者,下面是对参赛学生成绩的不完整统计.
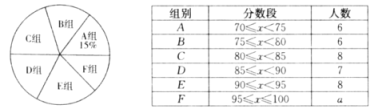
(1)统计表中,![]() =_____;各组人数的中位数是_____;统计图中,
=_____;各组人数的中位数是_____;统计图中,![]() 组所在扇形的圆心角是_____°;
组所在扇形的圆心角是_____°;
(2)李明同学得了88分,他说自己在参加选拔赛的同学中属于中午偏上水平,你认为他说的有道理吗?为什么?
(3)选出的10名优胜者中,男生、女生的分布情况如下表.
一班 | 二班 | 三班 | 四班 | 五班 | 六班 | |
男生人数 | 1 | 1 | 2 | 1 | 0 | 0 |
女生人数 | 1 | 0 | 0 | 2 | 1 | 1 |
若从中任选1名男生和1名女生代表学校参加全区的比赛,请有列表法或画树状图法求男生和女生都出在四班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与x轴交于点
与x轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)过第二象限的点![]() 作平行于x轴的直线,交直线
作平行于x轴的直线,交直线![]() 于点C,交函数
于点C,交函数![]() 的图象于点D.
的图象于点D.
①当![]() 时,判断线段PD与PC的数量关系,并说明理由;
时,判断线段PD与PC的数量关系,并说明理由;
②若![]() ,结合函数的图象,直接写出n的取值范围.
,结合函数的图象,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全国初中数学联赛中,将参赛两个班学生的成绩(得分均为整数)进行整理后分成五组,绘制出如下的频率分布直方图(如图所示),已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.25、0.15、0.10、0.10,第二组的频数是40.
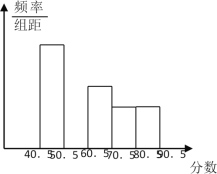
(1)第二小组的频率是_____,并补全这个频率分布直方图;
(2)这两个班参赛的学生人数是_________;
(3)这两个班参赛学生的成绩的中位数落在第______组内.(不必说明理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com