
【题目】如图,已知正方形ABCD,将一块等腰直角三角板的锐角顶点与A重合,并将三角板绕A点旋转,如图1,使它的斜边与BD交于点H,一条直角边与CD交于点G.
(1)请适当添加辅助线,通过三角形相似,求出![]() 的值;
的值;
(2)连接GH,判断GH与AF的位置关系,并证明;
(3)如图2,将三角板旋转至点F恰好在DC的延长线上时,若AD=![]() ,AF=
,AF=![]() .求DG的长.
.求DG的长.

【答案】(1)![]() ;(2)GH⊥AF,理由见解析;(3)
;(2)GH⊥AF,理由见解析;(3)![]()
【解析】试题分析:(1)连接AC,利用等量代换,求出∠BAH=∠GAC,再加上45的角,即可求出△BAH∽△CAG,进而得出结论;(2)先回答位置关系GH⊥AF,再证明,利用(1)问的结论,利用两边对应成比例且夹角相等得出△HAG∽△EAF,得出比例式即可;(3)判断出△AGD∽△FGE,得出![]() ,设出未知数,求出AG、EG的长度,利用相似即可求出DG的长度.
,设出未知数,求出AG、EG的长度,利用相似即可求出DG的长度.
试题解析:
(1)连接AC
∵四边形ABCD是正方形
∴∠BAC=∠ABH=∠ABH=45, ![]()
又∵△AEF是等腰直角三角形
∴∠EAH=45
∴∠BAH+∠EAC=∠FAC+∠EAC=45
∴∠BAH=∠GAC
∴△BAH∽△CAG.
∴![]()
(2)GH⊥AF,理由如下:
∵在Rt△AEF中, ![]()
∴![]()
又∵∠HAG=∠EAF
∴△HAG∽△EAF.
∴∠AHG=∠E=90
∴GH⊥AF..
(3)∵在Rt△AGH中, ![]()
∴AG=![]() GH
GH
又∵∠ADG=∠E=90,∠AGD=∠FGE
∴△AGD∽△FGE
∴![]() .
.
又∵在Rt△AEF中,AF=![]()
∴EF=5
∴![]()
∴![]()
∴![]()
∴可设GH为![]() ,则
,则![]()
∴AF=AH+FH=![]()
∴![]()
∴AG=![]() GH
GH![]()
∴![]()
又∵![]()
∴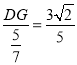
∴DG=![]()


科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于F,与DC的延长线相交于点H.
(1)求证:△BEF≌△CEH;
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据襄阳新闻报道2016年3月至2016年10月,襄阳闸口二路“大虾一条街”共销售大虾6000余吨.2017年潜江养虾专业户张小花抓住商机,将自己养殖的大虾销往襄阳.计算了养殖成本以及运费等诸多因素,他发现大虾的成本价为20元/公斤.经过市场调查,一周的销售量![]() 公斤与销售单价
公斤与销售单价![]() (
(![]() )元/公斤的关系如下表:
)元/公斤的关系如下表:
销售单价 | ... | 30 | 35 | 40 | 45 | ... |
销售量 | ... | 500 | 450 | 400 | 350 | ... |
(1)直接写出y与x的函数关系式;
(2)若张小花一周的销售利润为W元,请求出W与![]() 的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润随着销售单价的增大而增大?
的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润随着销售单价的增大而增大?
(3)随着赚的钱越来越多,张小花决定回馈社会将一周的销售利润全部捐给襄阳市福利院.若一周张小花的总成本不超过4000元,请求出张小花最大捐款数额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一粒大米的质量约为0.0000021千克,这个数用科学记数法表示为( )
A.0.21×10﹣5
B.2.1×10﹣5
C.2.1×10﹣6
D.21×10﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期实验中学组织开展课外兴趣活动,各活动小班根据实际情况确定了计划组班人数,并发动学生自愿报名,报名人数与计划人数的前5位情况如下.若用同一小班的报名人数与计划人数的比值大小来衡量进入该班的难易程度,则由表中数据,可预测( )
小班名称 | 奥数 | 写作 | 舞蹈 | 篮球 | 航模 |
报名人数 | 215 | 201 | 154 | 76 | 65 |
小班名称 | 奥数 | 舞蹈 | 写作 | 合唱 | 书法 |
计划人数 | 120 | 100 | 90 | 80 | 70 |
A. 奥数比书法容易
B. 合唱比篮球容易
C. 写作比舞蹈容易
D. 航模比书法容易
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com