
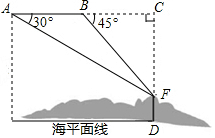
 国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航,如图,在一次巡航过程中,巡航飞机飞行高度为2274米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1400米到达B点后测得F点俯角为45°,请据此计算钓鱼岛的最高海拔高度.(结果保留根号)
国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航,如图,在一次巡航过程中,巡航飞机飞行高度为2274米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1400米到达B点后测得F点俯角为45°,请据此计算钓鱼岛的最高海拔高度.(结果保留根号) 分析 设CF=x,在Rt△ACF和Rt△BCF中,分别用CF表示AC、BC的长度,然后根据AC-BC=1200,求得x的值,用h-x即可求得最高海拔.
解答 解:设CF=x,
在Rt△ACF和Rt△BCF中,
∵∠BAF=30°,∠CBF=45°,
∴BC=CF=x,$\frac{CF}{AC}$=tan30°,
即AC=$\sqrt{3}$x,
∵AC-BC=1400米,
∴$\sqrt{3}$x-x=1400,
解得:x=700($\sqrt{3}$+1),
则DF=h-x=2274-700($\sqrt{3}$+1)=(1574-700$\sqrt{3}$)(米).
答:钓鱼岛的最高海拔高度约(1574-700$\sqrt{3}$)米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据俯角构造直角三角形求出AC、BC的长度,难度一般.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 6.8(1+2x)=9 | B. | 6.8(1+x)=9 | ||
| C. | 6.8+6.8(1+x)+6.8(1+x)2=9 | D. | 6.8(1+x)2=9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
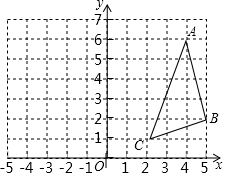 如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△A′B′C,那么点A、B的对应点A′、B′的坐标分别是( )
如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△A′B′C,那么点A、B的对应点A′、B′的坐标分别是( )| A. | (-3,3)、(-2,4) | B. | (3,-3)、(1,4) | C. | (3,-3)、(-2,4) | D. | (-3,3)、(1,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com