
【题目】如图,已知△ABC的三个顶点坐标为A(-2.3)、B(-6,0)、C(-1,0)
(1) 将△ABC绕坐标原点O旋转180°,画出图形,并写出点A的对应点A′ 的坐标________;
(2)将△ABC绕坐标原点O逆时针旋转90°,
直接写出点A的对应点A″的坐标___________;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标___________.

【答案】(1)(2,3);(2)(3,2);(3)(7,3)或(5,3)或(3,3).
【解析】分析:
(1)由题意先在坐标系中分别描出点A、B、C关于点O的对称点A′、B′、C′,再顺次连接描出的三个点即可得到所求图形,根据图形写出点A′的坐标即可;
(2)由题意先在坐标系中描出点A绕点O逆时针旋转90后对应的点A′′,根据图形写出点A′′的坐标即可;
(3)由题意在坐标系中画出以点A、B、C为顶点的平行四边形,根据图形写出其第4个顶点的坐标即可.
详解:
(1)如下图所示,图中的△A′B′C′是所求三角形;由图可得点A的对应点A′的坐标为:(2,3);
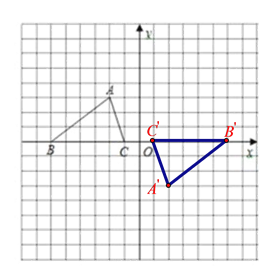
(2)如下图,点A的对应点A″的坐标(3,2);
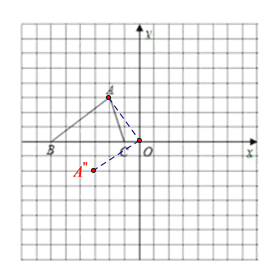
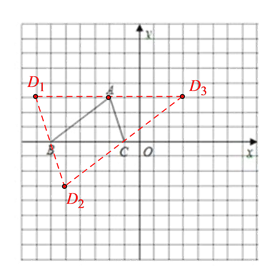
(3)如下图所示以A、B、C为顶点的平行四边形共有3个,其第四个顶点D的坐标分别为:(7,3)或(5,3)或(3,3).


科目:初中数学 来源: 题型:
【题目】已知点A,B是数轴上的点,且点A表示数-3,请参照图并思考,完成下列各题:
![]()
(1)将A点向右移动4个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是 .
(2)若把数轴绕点A对折,则对折后,点B落在数轴上的位置所表示的数为 .
(3)若(1)中点B以每秒2个单位长度沿数轴向左运动,A不动,多长时间后,点B与点A距离为2个单位长度?试列式计算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是边AC上一点,连BD,给出下列条件:①∠ABD=∠ACB;②AB2=ADAC;③ADBC=ABBD;④ABBC=ACBD.其中单独能够判定△ABC∽△ADB的个数是( ) 
A.①②
B.①②③
C.①②④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.

(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某国发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作,如图,某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米,参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5, ![]() ≈1.7)
≈1.7) 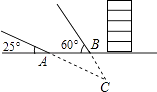
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读填空,并完成问题:“绝对值”一节学习后,数学老师对同学们的学习进行了拓展.数学老师向同学们提出了这样的问题:“在数轴上,一个数的绝对值就是表示这个数的点到原点的距离.那么,如果用P(a)表示数轴上的点P表示有理数a,Q(b)表示数轴上的点Q表示有理数b,那么点P与点Q的距离是多少?”
(1)聪明的小明经过思考回答说:这个问题应该有两种情况.一种是点P和点Q在原点的两侧,此时点P与点Q的距离是a和b的绝对值的和,即∣a∣+∣b∣.例如:点A(-3)与点B(5)的距离为∣-3∣+∣-5∣= ;
另一种是点P和点Q在原点的同侧,此时点P与点Q的距离的a和b中,较大的绝对值减去较小的绝对值,即∣a∣-∣b∣或∣b∣-∣a∣.例如:点A(-3)与点B(-5)的距离为∣-5∣-∣-3∣= ;
你认为小明的说法有道理吗?如果没有道理,请你指出错误之处;如果有道理,请你模仿求出数轴上点M(![]() )与N(
)与N(![]() )之间和点C(-2)与D(-7)之间的距离.
)之间和点C(-2)与D(-7)之间的距离.
(2)小颖在听了小明的方法后,提出了不同的方法,小颖说:我们可以不考虑点P和点Q所在的位置,无论点P与点Q的位置如何,它们之间的距离就是数a与b的差的绝对值,即∣a-b∣.例如:点A(-3)与点B(5)的距离就是∣-3-5∣= ;点A(-3)与点B(-5)的距离就是∣(-3)-(-5)∣= ;你认为小颖的说法有道理吗?如果没有道理,请你指出错误之处;如果有道理,请你模仿求出数轴上点M(![]() )与N(
)与N(![]() )之间和点C(-1.5)与D(-3.5)之间的距离.
)之间和点C(-1.5)与D(-3.5)之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点,
AC,E是AC的中点,
(1)求证:BC=DE;
(2)连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.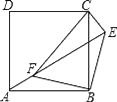
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com