练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图：BD平分∠ABC,F在AB上，G在AC上，FC与BD相交于点H.，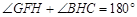
    求证： .

    证明见解析.

    解析试题分析：先证明FG∥BD，再利用角平分线的性质知∠2=∠ABD利用平行线的性质即得∠1=∠2.
    试题解析：∵∠BHC=∠DHF，且
    ∴
    ∴FG∥BD
    ∴∠1=∠ABD
    ∵BD平分∠ABC
    ∴∠ABD=∠2
    ∴∠1=∠2.
    考点：1.平行线的性质2.角平分线的性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

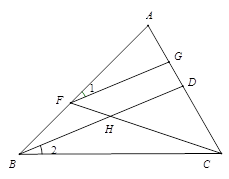
    已知：如图， AC∥DF，直线AF分别与直线BD、CE 相交于点G、H，∠1=∠2，
    求证: ∠C=∠D.
    解：∵∠1=∠2（已知）
    ∠1=∠DGH（                           ），
    ∴∠2=__   _______（ 等量代换  ）
    ∴       // ___________（ 同位角相等，两直线平行 ）
    ∴∠C=_          _( 两直线平行，同位角相等 )
    又∵AC∥DF（            ）
    ∴∠D=∠ABG (                           )
    ∴∠C=∠D (              )

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，C是线段AB的中点，CD∥BE，且CD=BE，求证：AD=CE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，直线AC∥DF，C、E分别在AB、DF上，小华想知道∠ACE和∠DEC是否互补，但是他有没有带量角器，只带了一副三角板，于是他想了这样一个办法：首先连结CF，再找出CF的中点O，然后连结EO并延长EO和直线AB相交于点B，经过测量，他发现EO＝BO，因此他得出结论：∠ACE和∠DEC互补，而且他还发现BC＝EF。

    以下是他的想法，请你填上根据。小华是这样想的：
    因为CF和BE相交于点O，
    根据                                  得出∠COB＝∠EOF；
    而O是CF的中点，那么CO＝FO，又已知 EO＝BO，                
    根据                                  得出△COB≌△FOE，   
    根据                                  得出BC＝EF，
    根据                                  得出∠BCO＝∠F，
    既然∠BCO＝∠F，根据                                              出AB∥DF，
    既然AB∥DF，根据                                           得出∠ACE和∠DEC互补.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图所示，已知AD⊥BC于点D，FE⊥BC于点E，交AB于点G，交CA的延长线于点F，且∠1=∠F．问：AD平分∠BAC吗？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图所示，已知直线AB及AB外一点C, 过点C作直线EF∥AB (要求：不写作法，保留作图痕迹)（5分）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，在直线CD上有一点P．
    （1）如果P点在C、D之间运动时，问∠PAC，∠APB，∠PBD有怎样的数量关系？请说明理由．(提示：过点P作PE∥l1) 
    （2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠PAC，∠APB，∠PBD之间的关系又是如何？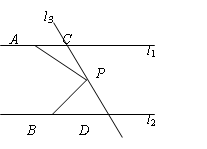

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    求证：两条直线被第三条直线所截，如果同旁内角的角平分线互相垂直， 那么这两条直线互相平行．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    如图，已知：AB∥CD，∠C=25°，∠E=30°，则∠A=　   　．

    查看答案和解析>>

    同步练习册答案