
【题目】在如图的2017年11月份的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )
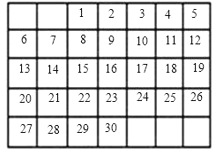
A.27B.51
C.69D.72
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】花果山是旅游胜地,据统计2014年9月30日花果山旅游人数为2万人, 十· 一黄金周期间,花果山7天中每天旅游人数的变化情况如下表(正数表示比9月30日多的人数,负数表示比9月30日少的人数):
![]()
(1)请判断7天内游客人数量最多和最少的各是哪一天?它们相差多少万人?
(2)求这7天去花果山旅游的总人数.
(3)如果去花果山旅游平均每人消费300元,求风景区在此7天内的总收入.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x![]() .
.
(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)?
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算;
,通过计算说明此时按哪种方案购买较为合算;
(3)当![]() 时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,开口向上的抛物线与![]() 轴交于
轴交于![]() 两点,
两点, ![]() 为抛物线的顶点,
为抛物线的顶点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() . 若
. 若![]() 的长分别是方程
的长分别是方程![]() 的两根,且
的两根,且![]()
(1)求抛物线对应的二次函数解析式和点![]() 的坐标。
的坐标。
(2)若点M为x轴正半轴上一个动点,N为线段AC上的一个动点,连接MN、CM,是否存在这样的点M,使△AMN为直角三角形和△CMN为等腰三角形同时成立,如果存在,请求出所有符合条件的点M的坐标,如果不存在,请说明理由。
(3如图2,过点![]() 任作直线
任作直线![]() 交线段
交线段![]() 于点
于点![]() 求
求![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,请直接写出
,请直接写出![]() 的最大值.
的最大值.

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂计划平均每天生产200辆,但是由于种种原因,实际每天生产量与计划量相比有出入。表是某周的生产情况(超产记为正,减产记为负):

(1)根据记录的数据可知该厂星期三生产自行车多少辆?
(2)产量最多的一天比产量最少的一天多生产自行车多少辆?
(3)根据记录的数据可知该厂本周实际共生产自行车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个“磁悬浮”的轨道架上做钢球碰撞实验,如图 1 所示,轨道长为 180![]() ,轨道架上有三个大小、质量完全相同的钢球
,轨道架上有三个大小、质量完全相同的钢球![]() 、
、![]() 、
、![]() ,轨道左右各有一个钢制挡板
,轨道左右各有一个钢制挡板 ![]() 和
和 ![]() ,其中
,其中![]() 到左挡板的距离为 30
到左挡板的距离为 30![]() ,
,![]() 到右挡板的距离为 60
到右挡板的距离为 60![]() ,
,![]() 、
、![]() 两球相距40
两球相距40![]() .现以轨道所在直线为数轴,假定
.现以轨道所在直线为数轴,假定![]() 球在原点,
球在原点,![]() 球代表的数为 40,如图 2 所示,解答下列问题:
球代表的数为 40,如图 2 所示,解答下列问题:

(1)在数轴上,找出 ![]() 球及右挡板
球及右挡板 ![]() 所代表的数,并填在图中括号内.
所代表的数,并填在图中括号内.

(2)碰撞实验中(钢球大小、相撞时间不记),钢球的运动都是匀速,当一钢球以一速度撞向另一静止钢球时,这个钢球停留在被撞钢球的位置,被撞钢球则以同样的速度向前运动,钢球撞到左右挡板则以相同的速度反向运动.
①现 ![]() 球以每秒 10
球以每秒 10![]() 的速度向右匀速运动,则
的速度向右匀速运动,则 ![]() 球第二次到达
球第二次到达![]() 球所在位置时用了 秒;经过 63 秒时,
球所在位置时用了 秒;经过 63 秒时,![]() 、
、![]() 、
、![]() 三球在数轴上所对应的数分别是 、 、 ;
三球在数轴上所对应的数分别是 、 、 ;
②如果![]() 、
、![]() 两球同时开始运动,
两球同时开始运动,![]() 球向左运动,
球向左运动,![]() 球向右运动,
球向右运动,![]() 球速度是每秒 8
球速度是每秒 8![]() ,
,![]() 球速度是每秒 12
球速度是每秒 12![]() ,问:经过多少时间
,问:经过多少时间 ![]() 、
、![]() 两球相撞?相撞时在数轴上所对应的数是多少?
两球相撞?相撞时在数轴上所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在体育活动课中,体育老师随机抽取了九年级甲、乙两班部分学生进行某体育项目的测试,并对成绩进行统计分析,绘制了频数分布表,请你根据表中的信息完成下列问题:
(1)频数分布表中a= ,b= ;
(2)如果该校九年级共有学生900人,估计该校该体育项目的成绩为良和优的学生有多少人?
(3)已知第一组中有两个甲班学生,第二组中只有一个乙班学生,老师随机从这两个组中各选一名学生对体育活动课提出建议,则所选两人正好是甲班和乙班各一人的概率是多少?
分 组 | 频数 | 频率 |
第一组(不及格) | 3 | 0.15 |
第二组(中) | b | 0.20 |
第三组(良) | 7 | 0.35 |
第四组(优) | 6 | a |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,先阅读再解决后面的问题:
原题:如图1,点E,F分别在正方形ABCD的边BC,CD上,![]() ,连接EF,求证:EF=BE+DF.
,连接EF,求证:EF=BE+DF.
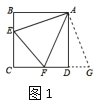
解题由于AB=AD,我们可以延长CD到点G,使DG=BE,易得![]() ,可证
,可证![]() .再证明
.再证明![]() ,得EF=FG=DG+FD=BE+DF.
,得EF=FG=DG+FD=BE+DF.
问题(1):如图2,在四边形ABCD中,AB=AD,![]() ,E,F分别是边BC,CD上的点,且
,E,F分别是边BC,CD上的点,且![]() ,求证:EF=BE+FD;
,求证:EF=BE+FD;

问题(2):如图3,在四边形ABCD中,![]() ,
,![]() ,AB=AD=1,点E,F分别在四边形ABCD的边BC,CD上的点,且
,AB=AD=1,点E,F分别在四边形ABCD的边BC,CD上的点,且![]() ,求此时
,求此时![]() 的周长
的周长

查看答案和解析>>
科目:初中数学 来源: 题型:
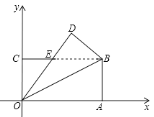
【题目】如图,矩形OABC的顶点与坐标原点O重合,将△OAB沿对角线OB所在的直线翻折,点A落在点D处,OD与BC相交于点E,已知OA=8,AB=4
(1)求证:△OBE是等腰三角形;
(2)求E点的坐标;
(3)坐标平面内是否存在一点P,使得以B,D,E,P为顶点的四边形是平行四边形?若存在,请直接写出P点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com