
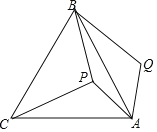
【题目】如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60得到线段AQ,连接BQ,若PA=3,PB=4,PC=5,则四边形APBQ的面积为_____
【答案】![]()
【解析】
连结PQ,如图,根据等边三角形的性质得∠BAC=60°,AB=AC,再根据旋转的性质得AP=PQ=3,∠PAQ=60°,则可判断△APQ为等边三角形,所以PQ=AP=3,接着证明△APC≌△ABQ得到PC=QB=5,然后利用勾股定理的逆定理证明△PBQ为直角三角形,再根据三角形面积公式,利用S四边形APBQ=S△BPQ+S△APQ进行计算.
连结PQ,如图,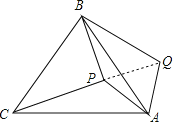
∵△ABC为等边三角形,
∴∠BAC=60°,AB=AC,
∵线段AP绕点A顺时针旋转60°得到线段AQ,
∴AP=PQ=3,∠PAQ=60°,
∴△APQ为等边三角形,
∴PQ=AP=3,
∵∠CAP+∠BAP=60°,∠BAP+∠BAQ=60°,
∴∠CAP=∠BAQ,
在△APC和△ABQ中,
∵AC=AB,
∠CAP=∠BAQ,
AP=AQ,
∴△APC≌△ABQ(SAS),
∴PC=QB=5,
在△BPQ中,∵PB2=42=16,PQ2=32=9,BQ2=52=25,
而16+9=25,
∴PB2+PQ2=BQ2,
∴△PBQ为直角三角形,∠BPQ=90°,
∴S四边形APBQ=S△BPQ+S△APQ=![]() ×3×4+
×3×4+![]() ×32=
×32=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,∠MPN为直角,使点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:①EF=![]() OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF=
OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF=![]() OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;⑤OGBD=AE2+CF2.其中结论正确的个数是( )
;⑤OGBD=AE2+CF2.其中结论正确的个数是( )
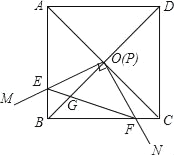
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
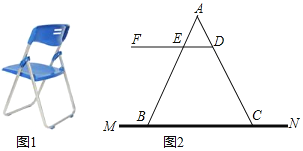
【题目】如图1是一种折叠椅,忽略其支架等的宽度,得到他的侧面简化结构图![]() 图
图![]() ,支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得
,支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得![]() 厘米,
厘米, ![]() 厘米,
厘米, ![]() .
.
![]() 求椅子的高度
求椅子的高度![]() 即椅子的座板DF与地面MN之间的距离
即椅子的座板DF与地面MN之间的距离![]() 精确到1厘米
精确到1厘米![]()
![]() 求椅子两脚B、C之间的距离
求椅子两脚B、C之间的距离![]() 精确到1厘米
精确到1厘米![]() 参考数据:
参考数据: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行了调查,随机调查了![]() 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.

(1)根据图中信息求出![]() =___________,
=___________,![]() =_____________;
=_____________;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生种,大约有多少人最认可“微信”这一新生事物?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AC=BC,以BC为直径的⊙O交AB于点D.
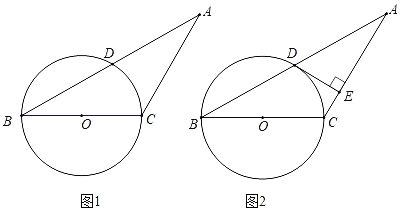
(1)求证:点D是AB的中点;
(2)如图2,过点D作DE⊥AC于点E,求证:DE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2k-1)x+k2=0有两个实根x1和x2
(1) 求实数k的取值范围
(2) 若方程两实根x1、x2满足x12-x22=0,求k的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,![]() )三点.
)三点.

(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com