
分析 (1)根据顶点坐标,可得方程组,根据解方程组,可得答案;
(2)根据三边对应相等的两个三角形全等,可得PB=PD,根据方程,可得答案;
(3)根据an+1=an+1,可得A2017坐标,根据图象平移规律,可得B点,根据线段中点公式,可得A2017B的中点,根据到与直线的距离,可得圆心到直线的距离,根据勾股定理,可得A2017B的长,根据圆心到直线的距离小于半径,可得答案.
解答  解:(1)∵a1=1,
解:(1)∵a1=1,
∴C1的顶点为(1,-4),
则$\left\{\begin{array}{l}{-\frac{b}{2}=1}\\{\frac{4c-{b}^{2}}{4}=-4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,
所以抛物线C1的解析式是:y=x2-2x-3;
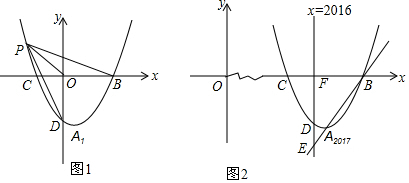
(2)如图1,设P(x,(x-1)2-4),当x=0时,y=-3,即D(0,-3),
当y=0时,x2-2x-3=0,解得x=3或x=-1,即B(3,0),
OB=OD,PO=PO,当PB=PD时,△POB≌△POD,
(x-3)2+[(x-1)2-4]2=x2+[(x-1)2-4+3]2,
化简,得x2-x-3=0,
解得x1=$\frac{1+\sqrt{13}}{2}$,x2=$\frac{1-\sqrt{13}}{2}$,
y1=$\frac{-1-\sqrt{13}}{2}$,y2=$\frac{-1+\sqrt{13}}{2}$,
P1($\frac{1+\sqrt{13}}{2}$,$\frac{-1-\sqrt{13}}{2}$),P2($\frac{1-\sqrt{13}}{2}$,$\frac{-1+\sqrt{13}}{2}$);
(3)如图2,A2016(2017,-4),B(2019,0),A2016B的中点O(2018,-2)
O到直线x=2016距离为2018-2016=2,
而圆的半径为$\frac{{A}_{2016}B}{2}$=$\frac{\sqrt{(2019-2017)^{2}+(0+4)^{2}}}{2}$=$\sqrt{5}$,
因为2<$\sqrt{5}$,
所以直线x=2016与圆相交.
点评 本题考查了二次函数综合题,(1)利用顶点坐标公式得出方程组是解题关键;(2)利用三角形全等的条件得出PB=PD是解题关键;(3)利用图象平移规律得出A2016、B点坐标是解题关键,又利用了直线与圆的位置关系.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 我爱美 | B. | 蒙城游 | C. | 爱我蒙城 | D. | 美我蒙城 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
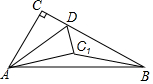 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=6,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点C1处,连接C1B,则BC1的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=6,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点C1处,连接C1B,则BC1的最小值为( )| A. | 2 | B. | 3 | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com