练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

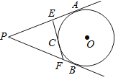
    【题目】如图，、分别切于、，，是劣弧上的点（不与点、重合），过点的切线分别交、于点、．则的周长为（ ）

    A. B. C. D.

    【答案】C

    【解析】

    根据切线长定理由PA、PB分别切⊙O于A、B得到PB=PA=10cm，由于过点C的切线分别交PA、PB于点E、F，再根据切线长定理得到EA=EC，FC=FB，然后三角形周长的定义得到△PEF的周长=PE+EF+PF=PE+EC+FC+PF，用等线段代换后得到三角形PEF的周长等于PA+PB即可得答案.

    ∵PA、PB分别切⊙O于A、B，

    ∴PB=PA=10cm，

    ∵EA与EC为⊙的切线，

    ∴EA=EC，

    同理得到FC=FB，

    ∴△PEF的周长=PE+EF+PF=PE+EC+FC+PF

    =PE+EA+FB+PF

    =PA+PB

    =10+10

    =20（cm）．

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，直线l1：y＝kx+b与x轴、y轴分别交于A，B两点，其中点B的坐标为（0，6），∠BAO=30°将直线l1沿着y轴正方向平移一段距离得到直线l2交y轴于点M，且l1与l2之间的距离为3，点C（x，y）是直线11上的一个动点，过点C作AB的垂线CD交y轴于点D．

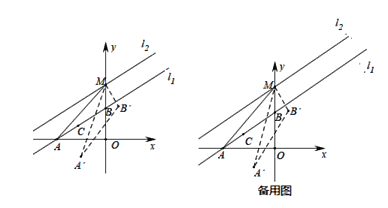
    （1）求点M的坐标和直线l1的解析式；

    （2）当C运动到什么位置时，△AOD的面积为21，求出此时点C的坐标；

    （3）连接AM，将△ABM绕着点M旋转得到△A'B'M，在平面内是否存在一点N．使四边形AMA'N为矩形？若存在，求出点N的坐标：若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

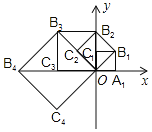
    【题目】如图，在平面直角坐标系中，边长为1的正方形OA1B1C1的两边在坐标轴上，以它的对角线OB1为边作正方形OB1B2C2，再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3，以此类推……则正方形OB2019B2020C2020的顶点B2020的坐标是 _____.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

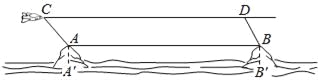
    【题目】如图，某海域有两个海拔均为200米的海岛A和海岛B，一勘测飞机在距离海平面垂直高度为1100米的空中飞行，飞行到点C处时测得正前方一海岛顶端A的俯角是45°，然后沿平行于AB的方向水平飞行1.99×104米到达点D处，在D处测得正前方另一海岛顶端B的俯角是60°，求两海岛间的距离AB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列条件中，不能判断是直角三角形的是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，为的直径，点在上，延长至点，使，延长与的另一个交点为，连接，．

    求证：；

    若，，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，、切于、，是弧上任一点，过点作的切线交、于点、．

    若，求的周长；

    若，，，你能求出的半径吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点D在AB上，点E在AC上，AB＝AC添加下列一个条件后，还不能证明△ABE≌△ACD的是（　　）

    A.AD＝AEB.BD＝CEC.∠B＝∠CD.BE＝CD

    查看答案和解析>>

    科目：初中数学 来源： 题型：

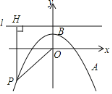
    【题目】如图，在平面直角坐标系中，抛物线经过点，顶点为点，点为抛物线上的一个动点，是过点且垂直于轴的直线，过作，垂足为，连接．

    求抛物线的解析式，并写出其顶点的坐标；

    ①当点运动到点处时，计算：________，________，由此发现，________（填“”、“”或“”）；

    ②当点在抛物线上运动时，猜想与有什么数量关系，并证明你的猜想．

    查看答案和解析>>

    同步练习册答案