解答下列问题:
(1)在一个不透明的口袋中有10个红球和若干个白球,这些球除颜色不同外其他都相同,请通过以下实验估计口袋中白球的个数:从口袋中随机摸出一球,记下颜色,再把它放回袋中,不断重复上述过程,实验总共摸了200次,其中有50次摸到了红球,那么估计口袋中有白球多少个?
(2)请思考并作答:
在一个不透明的口袋里装有若干个形状、大小完全相同的白球,在不允许将球倒出来的情况下,如何估计白球的个数(可以借助其它工具及用品)?写出解决问题的主要步骤及估算方法,并求出结果(其中所需数量用a、b、c 等字母表示).
【答案】
分析:(1)根据口袋中有10个红球,利用小球在总数中所占比例得出与实验比例应该相等求出即可;
(2)利用做标记的方法,得出带标记的小球在总数中所占比例应该等于实验比例求出即可.
解答:解:(1)∵实验总共摸了200次,其中有50次摸到了红球,
∵口袋中有10个红球,假设有x个白球,
∴
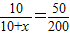
,
解得:x=30,
∴口袋中有白球30个;
(2)可以拿出a个标上记号,然后搅匀后再拿出b个,带记号的有c个,即可估计白球的个数.
设球的总个数为x,
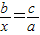
,
∴x=
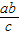
.
∴白球的个数为

.
点评:此题主要考查了常用的模拟试验的方法,根据已知得出小球在总数中所占比例得出与实验比例应该相等是解决问题的关键.

 图的信息解答下列问题.
图的信息解答下列问题.