
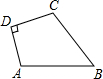
 某农户有一不规则四边形田地(如图).已知 AD=3m,DC=4m,BC=12m,AB=13m,且测得∠ADC为一直角,试计算这块田的面积为
某农户有一不规则四边形田地(如图).已知 AD=3m,DC=4m,BC=12m,AB=13m,且测得∠ADC为一直角,试计算这块田的面积为 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:1+1轻巧夺冠·优化训练·八年级数学下 题型:044
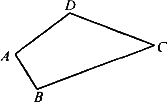
如图,某农户有一口呈四边形的池塘,在池塘的四个角A、B、C、D处均有一棵果树.为了扩大池塘养殖面积,该农户准备把原来的池塘面积扩大一倍,且要求扩大池塘面积后原来的果树保持不动,你能帮助农户设计一个方案并画出图形.
查看答案和解析>>
科目:初中数学 来源:湖北省期末题 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
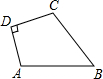 某农户有一不规则四边形田地(如图).已知 AD=3m,DC=4m,BC=12m,AB=13m,且测得∠ADC为一直角,试计算这块田的面积为________ m2.
某农户有一不规则四边形田地(如图).已知 AD=3m,DC=4m,BC=12m,AB=13m,且测得∠ADC为一直角,试计算这块田的面积为________ m2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com