
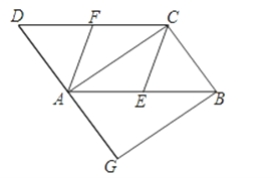
【题目】如图,在平面直角坐标系中,已知两点A(m,0),B(0,n)(n>m>0),点C在第一象限,AB⊥BC,BC=BA,点P在线段OB上,OP=OA,AP的延长线与CB的延长线交于点M,AB与CP交于点N.

(1)点C的坐标为: (用含m,n的式子表示);
(2)求证:BM=BN;
(3)设点C关于直线AB的对称点为D,点C关于直线AP的对称点为G,求证:D,G关于x轴对称.
【答案】(1)(n,m+n);(2)见解析;(3)见解析
【解析】
试题分析:(1)过C点作CE⊥y轴于点E,根据AAS证明△AOB≌△BEC,根据全等三角形的性质即可得到点C的坐标;
(2)根据全等三角形的性质的性质和等量代换可得∠1=∠2,根据ASA证明△ABM≌△CBN,根据全等三角形的性质即可得到BM=BN;
(3)根据SAS证明△DAH≌△GAH,根据全等三角形的性质即可求解.
(1)解:过C点作CE⊥y轴于点E,
∵CE⊥y轴,
∴∠BEC=90°,
∴∠BEC=∠AOB,
∵AB⊥BC,
∴∠ABC=90°,
∴∠ABO+∠CBE=90°,
∵∠ABO+∠BAO=90°,
∴∠CBE=∠BAO,
在△AOB与△BEC中,
 ,
,
∴△AOB≌△BEC(AAS),
∴CE=OB=n,BE=OA=m,
∴OE=OB+BE=m+n,
∴点C的坐标为(n,m+n).
故答案为:(n,m+n);
(2)证明:∵△AOB≌△BEC,
∴BE=OA=OP,CE=BO,
∴PE=OB=CE,
∴∠EPC=45°,
∠APC=90°,
∴∠1=∠2,
在△ABM与△CBN中,
 ,
,
∴△ABM≌△CBN(ASA),
∴BM=BN;
(3)证明:∵点C关于直线AB的对称点为D,点C关于直线AP的对称点为G,
∴AD=AC,AG=AC,
∴AD=AG,
∵∠1=∠5,∠1=∠6,
∴∠5=∠6,
在△DAH与△GAH中,
 ,
,
∴△DAH≌△GAH(SAS),
∴D,G关于x轴对称.



科目:初中数学 来源: 题型:
【题目】某个体经营户销售同一型号的A、B两种品牌的服装,平均每月共销售60件,已知两种品牌的成本和利润如表所示,设平均每月的利润为y元,每月销售A品牌x件.
(1)写出y关于x的函数关系式.
(2)如果每月投入的成本不超过6500元,所获利润不少于2920元,不考虑其他因素,那么销售方案有哪几种?
(3)在(2)的条件下要使平均每月利润率最大,请直接写出A、B两种品牌的服装各销售多少件?
A | B | |
成本(元/件) | 120 | 85 |
利润(元/件) | 60 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,AC是对角线,过点B作BG∥AC交DA的延长线于点G.
(1)求证:CE∥AF;
(2)若∠G=90°,求证:四边形CEAF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC与BD相交于点O,∠D=∠C,添加下列哪个条件后,仍不能使△ADO≌△BCO的是( )

A. AD=BC B. AC=BD C. OD=OC D. ∠ABD=∠BAC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)
若A,B,C为数轴上三点,若点C到A的距离是点C到B的距离的2倍,我们就称点C是(A,B)的优点.
例如,如图①,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的优点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的优点,但点D是(B,A)的优点.
(知识运用)
如图②,M、N为数轴上两点,点M所表示的数为﹣2,点N所表示的数为4.
(1)数 所表示的点是(M,N)的优点;
(2)如图③,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以4个单位每秒的速度向左运动,到达点A停止.当t为何值时,P、A和B中恰有一个点为其余两点的优点?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运动时心跳速率通常和人的年龄有关。用a表示一个人的年龄,用b表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数,则![]() .
.

(1)正常情况下,一个14岁的少年运动时所能承受的每分钟心跳的最高次数是多少?
(2)当一个人的年龄增加10岁时,他运动时承受的每分钟心跳最高次数有何变化?变化次数是多少?
(3)一个45岁的人运动时,10秒心跳次数为22次,请问他有危险吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下面的程序计算,当输入x=100时,输出结果为501;当输入x=20时,输出结果为506;如果开始输入的值x为正数,最后输出的结果为656,那么满足条件的x的值最多有( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践操作:在矩形ABCD中,AB=4,AD=3,现将纸片折叠,点D的对应点记为点P,折痕为EF(点E、F是折痕与矩形的边的交点),再将纸片还原.
初步思考:
(1)若点P落在矩形ABCD的边AB上(如图①)
①当点P与点A重合时,∠DEF= °;当点E与点A重合时,∠DEF= °;
②当点E在AB上,点F在DC上时(如图②),
求证:四边形DEPF为菱形,并直接写出当AP=3.5时的菱形EPFD的边长.

深入探究
(2)若点P落在矩形ABCD的内部(如图③),且点E、F分别在AD、DC边上,请直接写出AP的最小值 .
拓展延伸
(3)若点F与点C重合,点E在AD上,线段BA与线段FP交于点M(如图④).在各种不同的折叠位置中,是否存在某一情况,使得线段AM与线段DE的长度相等?若存在,请直接写出线段AE的长度;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com