
【题目】如图,以△ABC的边BC为直径作⊙O,点A在⊙O上,点D在线段BC的延长线上,AD=AB,∠D=30°.
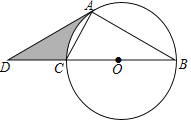
(1)求证:直线AD是⊙O的切线;
(2)若直径BC=8,求图中阴影部分的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OA,则得出∠COA=2∠B=2∠D=60°,可求得∠OAD=90°,可得出结论;
(2)可利用△OAD的面积扇形AOC的面积求得阴影部分的面积.
(1)证明:连接OA,则∠COA=2∠B,
∵AD=AB,∠D=30°,
∴∠B=∠D=30°,
∴∠COA=60°,
∴∠OAD=180°60°30°=90°,
∴OA⊥AD,
即CD是⊙O的切线; 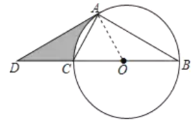
(2)解:∵BC=8,
∴OA=OC=4,
在Rt△OAD中,OA=4,∠D=30°,
∴OD=2OA=8,AD=![]() ,
,
所以S△OAD=![]() OAAD=
OAAD=![]() ×4×
×4×![]() =
=![]() ,
,
因为∠COA=60°,
所以S扇形COA=![]() ,
,
所以S阴影=S△OADS扇形COA=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,已知格点四边形ABCD(顶点是网格线的交点)和格点O.

(1)将四边形ABCD先向左平移4个单位长度,再向下平移6个单位长度,得到四边形A1B1C1D1,画出平移后的四边形A1B1C1D1,(点A,B,C,D的对应点分别为点A1,B1,C1,D1);
(2)将四边形ABCD绕点O逆时针旋转90°,得到四边形A2B2C2D2,画出旋转后的四边形A2B2C2D2(点A、B,C,D的对应点分别为点A2,B2,C2,D2);
(3)填空:点C2到A1D1的距离为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A点的坐标为(﹣1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐 标为(3,﹣1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图![]() 、图
、图![]() 分别是
分别是![]() 的网格,网格中的每个小正方形的边长均为1,点
的网格,网格中的每个小正方形的边长均为1,点![]() 、
、![]() 、
、![]() 、
、![]() 在小正方形的顶点上.请在网格中按要求画出图形:
在小正方形的顶点上.请在网格中按要求画出图形:
(1)在图![]() 中画以
中画以![]() 为斜边的直角三角形
为斜边的直角三角形![]() (点
(点![]() 在小正方形的顶点上),使得
在小正方形的顶点上),使得![]() ;
;
(2)在图![]() 中画以
中画以![]() 为边的四边形
为边的四边形![]() (点
(点![]() 、
、![]() 在小正方形的顶点上),使得四边形
在小正方形的顶点上),使得四边形![]() 是中心对称图形但不是轴对称图形,且
是中心对称图形但不是轴对称图形,且![]() ,并直接写出四边形
,并直接写出四边形![]() 的面积.
的面积.

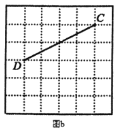
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A. ![]() B.
B. ![]() C.
C.![]()
![]() D.
D. ![]()
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A、B的坐标分别是A(3,2)、B(1,3).

(1)将△AOB向下平移3个单位后得到△A1O1B1,则点B1的坐标为 ;
(2)将△AOB绕点O逆时针旋转90°后得到△A2OB2,请在图中作出△A2OB2,并求出这时点A2的坐标为 ;
(3)在(2)中的旋转过程中,线段OA扫过的图形的面积 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了方便学生在上下学期间安全过马路,南岸区政府决定在南开(融侨)中学校门口修建人行天桥(如图1),其平面图如图2所示,初三(8)班的学生小刘想利用所学知识测量天桥顶棚距地面的高度.天桥入口A点有一台阶AB=2m,其坡角为30°,在AB上方有两段平层BC=DE=1.5m,且BC,DE与地面平行,BC,DE上方又紧接台阶CD,EF,其长度相等且坡度均为i=4:3,顶棚距天桥距离FG=2m,且小刘从入口A点测得顶棚顶端G的仰角为37°,请根据以上数据,帮小刘计算出顶端G点距地面高度为( )m.(结果保留一位小数,参考数据:![]() ≈1.73,sin37°≈
≈1.73,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
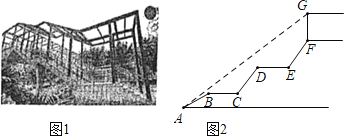
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
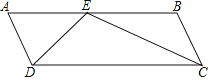
【题目】如图,在平行四边形ABCD中,∠B=120°,AB与CD之间的距离是![]() ,AB=28,在AB上取一点E(AE<BE),使得∠DEC=120°,则AE=_____.
,AB=28,在AB上取一点E(AE<BE),使得∠DEC=120°,则AE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
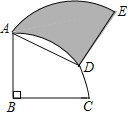
【题目】如图,将半径为4,圆心角为90°的扇形BAC绕A点逆时针旋转60°,点B、C的对应点分别为点D、E且点D刚好在![]() 上,则阴影部分的面积为_____.
上,则阴影部分的面积为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com