
【题目】在![]() 中,
中,![]() ,
,![]() 的垂直平分线与
的垂直平分线与![]() 所在的直线相交所得到的锐角为
所在的直线相交所得到的锐角为![]() ,则
,则![]() 等于______________度.
等于______________度.
【答案】65°或25°
【解析】
(1)当△ABC是锐角三角形时,根据题目条件得到∠A=50°,利用△ABC是等腰三角形即可求解;(2)当△ABC是钝角三角形时,同理可得即可得出结果.
解:(1)当△ABC是锐角等腰三角形时,如图1所示
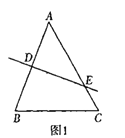
由题知:DE⊥AB,AD=DB,∠AED=40°
∴∠A=180°-90°-40°=50°
∵AB=AC
∴△ABC是等腰三角形
∴∠ABC=∠ACB
∴∠ABC=(180°-50°)÷2=65°
(2)当△ABC是钝角三角形时,如图2所示
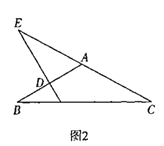
由题知:DE⊥AB,AD=DB,∠AED=40°
∴∠AED+∠ADE=∠BAC
∴∠BAC=90°+40°=130°
∵AB=AC
∴△ABC是等腰三角形
∴∠ABC=∠ACB
∴∠ABC=(180°-130°)÷2=25°
∴∠ABC=65°或25°
故答案为:65°或25°


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC=CA,∠A=∠ABC=∠ACB,在△ABC的顶点A,C处各有一只小蚂蚁,它们同时出发,分别以相同速度由A向B和由C向A爬行,经过t(s)后,它们分别爬行到了D,E处,设DC与BE的交点为F.

(1)△ACD≌△CBE吗?为什么?
(2)小蚂蚁在爬行过程中,DC与BE所成的∠BFC的大小有无变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,某公交公司决定购买A、B两种型号的全新混合动力公交车共10辆,其中A种型号每辆价格为a万元,每年节省油量为![]() 万升;B种型号每辆价格为b万元,每年节省油量为
万升;B种型号每辆价格为b万元,每年节省油量为![]() 万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
![]() 请求出a和b;
请求出a和b;
![]() 若购买这批混合动力公交车每年能节省
若购买这批混合动力公交车每年能节省![]() 万升汽油,求购买这批混合动力公交车需要多少万元?
万升汽油,求购买这批混合动力公交车需要多少万元?
【答案】(1)![]() ;(2)购买这批混合动力公交车需要1040万元.
;(2)购买这批混合动力公交车需要1040万元.
【解析】
(1)根据“购买一台A型车比购买一台B型车多20万元,购买2台A型车比购买3台B型车少60万元.”即可列出关于a、b的二元一次方程组,解之即可得出结论;
(2)设A型车购买x台,B型车购买y台,根据总节油量=2.4×A型车购买的数量+2.2×B型车购买的数量、A型车数量+B型车数量=10得出方程组,解之求得x和y的值,再根据总费用=120×A型车购买的数量+100×B型车购买的数量即可算出购买这批混合动力公交车的总费用.
解:![]() 根据题意得:
根据题意得:![]() ,
,
解得:![]() ;
;
![]() 设A型车购买x台,B型车购买y台,
设A型车购买x台,B型车购买y台,
根据题意得:![]() ,
,
解得:![]() ,
,
![]() 万元
万元![]() .
.
答:购买这批混合动力公交车需要1040万元.
【点睛】
本题考查了二元一次方程组的应用,根据题意找出等量关系列出方程组是解题的关键.
【题型】解答题
【结束】
16
【题目】在边长为1的正方形网格中
![]() 作出
作出![]() 关于直线MN对称的
关于直线MN对称的![]() ;
;
![]() 若
若![]() 经过图形平移得到
经过图形平移得到![]() ,当点A的坐标是
,当点A的坐标是![]() 时,请建立适当的直角坐标系,分别写出点
时,请建立适当的直角坐标系,分别写出点![]() ,
,![]() ,
,![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(14分)盘锦红海滩景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用![]() (元)及节假日门票费用
(元)及节假日门票费用![]() (元)与游客x(人)之间的函数关系如图所示.
(元)与游客x(人)之间的函数关系如图所示.

(1)a= ,b= ;
(2)直接写出![]() 、
、![]() 与x之间的函数关系式;
与x之间的函数关系式;
(3)导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到红海滩景区旅游,两团共计50人,两次共付门票费用3040元,求A、B两个旅游团各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,E为AC的中点,AD平分∠BAC,BA:CA=2:3,AD与BE相交于点O,若△OAE的面积比△BOD的面积大1,则△ABC的面积是( )

A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场的一种书法笔每只售价25元,书法练习本每本售价5元。为促销,商场制定了两种优惠方案:买一支书法笔就赠送一本书法练习本;方案二:按够买金额的九折付款,我校书法社团够买10支书法笔,x(x>10)本练习本。
(1)请你写出两种优惠方案的实际付款金额y(元)与x(本)之间的关系式。
(2)当购买多少本书法练习本时,两种优惠方案的实付金额一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com