
分析 观察等式左边的特点,即第几个式子就是几分之(几加1)乘以自己的分子;右边的特点即左边两个因数相加.
解答 解:∵$\frac{2}{1}$×2=$\frac{2}{1}$+2;
$\frac{3}{2}$×3=$\frac{3}{2}$+3;
$\frac{4}{3}$×4=$\frac{4}{3}$+4;
$\frac{5}{4}$×5=$\frac{5}{4}$+5,
…
∴$\frac{n+1}{n}$×(n+1)=$\frac{n+1}{n}$+n+1,
故答案为:$\frac{n+1}{n}$×(n+1)=$\frac{n+1}{n}$+n+1.
点评 此题考查数字的变化规律,通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.该规律实质上是运用了分式的加法运算法则.


科目:初中数学 来源: 题型:选择题
| A. | (-1,-2) | B. | (-1,2) | C. | (1,-2) | D. | (-2,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线上一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.
如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线上一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
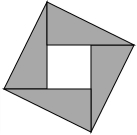 2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )| A. | 25 | B. | 19 | C. | 13 | D. | 169 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
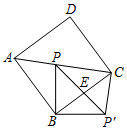 如图,正方形ABCD的边长是7$\sqrt{2}$,点P是对角线AC上的一个点(不与A,C两点重合),连接BP,并将线段BP绕点B顺时针旋转90°得到线段BP′,连接PP′,CP′,PP′与BC相交于点E.
如图,正方形ABCD的边长是7$\sqrt{2}$,点P是对角线AC上的一个点(不与A,C两点重合),连接BP,并将线段BP绕点B顺时针旋转90°得到线段BP′,连接PP′,CP′,PP′与BC相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}a+b=1\\ 2a+b=4\end{array}\right.$ | B. | $\left\{\begin{array}{l}3a+b=3\\ 2a+b=4\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}a+b=1\\ 3a-2c=19\end{array}\right.$ | D. | $\left\{\begin{array}{l}5a-2b=19\\ 3a+b=3\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
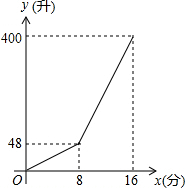 一个容积为400升的水箱,安装A、B两个进水管向水箱注水,注水过程中A水管始终打开,两水管进水的速度保持不变,当水箱注满时,两水管自动停止注水,注水过程中水箱中水量y(升)与A管注水时间x(分)之间的函数图象如图所示.
一个容积为400升的水箱,安装A、B两个进水管向水箱注水,注水过程中A水管始终打开,两水管进水的速度保持不变,当水箱注满时,两水管自动停止注水,注水过程中水箱中水量y(升)与A管注水时间x(分)之间的函数图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com