
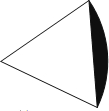
 如图,已知扇形的圆心角为60°,半径为$\sqrt{3}$,则图中弓形的面积为$\frac{2π-3\sqrt{3}}{4}$.
如图,已知扇形的圆心角为60°,半径为$\sqrt{3}$,则图中弓形的面积为$\frac{2π-3\sqrt{3}}{4}$. 分析 过A作AD⊥CB,首先计算出BC上的高AD长,再计算出三角形ABC的面积和扇形面积,然后再利用扇形面积减去三角形的面积可得弓形面积.
解答  解:过A作AD⊥CB,
解:过A作AD⊥CB,
∵∠CAB=60°,AC=AB,
∴△ABC是等边三角形,
∵AC=$\sqrt{3}$,
∴AD=AC•sin60°=$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=$\frac{3}{2}$,
∴△ABC面积:$\frac{1}{2}×$$\sqrt{3}$×$\frac{3}{2}$=$\frac{3\sqrt{3}}{4}$,
∵扇形面积:$\frac{60•π•3}{360}$=$\frac{π}{2}$,
∴弓形的面积为:$\frac{π}{2}$-$\frac{3\sqrt{3}}{4}$=$\frac{2π-3\sqrt{3}}{4}$,
故答案为:$\frac{2π-3\sqrt{3}}{4}$.
点评 此题主要考查了扇形面积的计算,关键是掌握扇形的面积公式:S=$\frac{nπ{r}^{2}}{360}$.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC在直角坐标系中
如图,△ABC在直角坐标系中查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
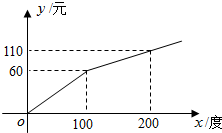 电力资源丰富,并且得到了较好的开发.某地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的函数图象如图.
电力资源丰富,并且得到了较好的开发.某地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的函数图象如图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
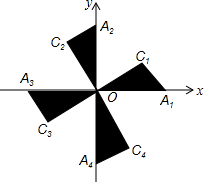 如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依次规律,点A2016的纵坐标为( )
如图,在平面直角坐标系xOy中,Rt△OA1C1,Rt△OA2C2,Rt△OA3C3,Rt△OA4C4…的斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3=∠A4OC4…=30°.若点A1的坐标为(3,0),OA1=OC2,OA2=OC3,OA3=OC4…,则依次规律,点A2016的纵坐标为( )| A. | 0 | B. | -3×($\frac{2}{3}$$\sqrt{3}$)2015 | C. | (2$\sqrt{3}$)2016 | D. | 3×($\frac{2}{3}$$\sqrt{3}$)2015 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com