
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE,其中正确结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
【答案】C
【解析】∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°.
∵△AEF等边三角形,
∴AE=EF=AF,∠EAF=60°.
∴∠BAE+∠DAF=30°.
在Rt△ABE和Rt△ADF中,
![]() ,
,
Rt△ABE≌Rt△ADF(HL),
∴BE=DF(故①正确).
∠BAE=∠DAF,
∴∠DAF+∠DAF=30°,
即∠DAF=15°(故②正确),
∵BC=CD,
∴BC-BE=CD-DF,即CE=CF,
∵AE=AF,
∴AC垂直平分EF.(故③正确).
设EC=x,由勾股定理,得
EF=![]() x,CG=
x,CG=![]() x,
x,
AG=AEsin60°=EFsin60°=2×CGsin60°=![]() x,
x,
∴AC= ![]() ,
,
∴AB= ![]() ,
,
BE= ![]() ,
,
∴BE+DF= ![]() ≠
≠![]() x,(故④错误),
x,(故④错误),
∵S△CEF=![]() ,
,
S△ABE=![]() ,
,
∴2S△ABE=![]() =S△CEF,(故⑤正确).
=S△CEF,(故⑤正确).
综上所述,正确的有4个,
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,有一圆柱,其高为12cm,它的底面半径为3cm,在圆柱下底面A处有一只蚂蚁,它想得到上面B处的食物,则蚂蚁经过的最短距离为_________.(π取3)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD,AB=9,AD=4. E为CD边上一点,CE=6.
(1)求AE的长.
(2)点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE. 设点P运动的时间为t秒,则当t为何值时,△PAE为等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
![]()
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察探索:
(x﹣1)(x+1)=x2﹣1
(x﹣1)(x2+x+1)=x3﹣1
(x﹣1)(x3+x2+x+1)=x4﹣1
(x﹣1)(x4+x3+x2+x+1)=x5﹣1
根据规律填空:(x﹣1)(xn+xn﹣1+…+x+1)=__.(n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
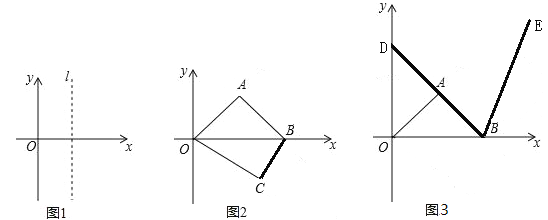
【题目】(1)观察与归纳:在如图1所示的平面直角坐标系中,直线l与y轴平行,点M与点N 是直线l上的两点(点M在点N的上方).
①亮亮发现:若点M坐标为(2,3),点N坐标为(2,﹣4),则MN的长度为_____; ②亮亮经过多次取l上的两点后,他归纳出这样的结论:若点M坐标为(t,m),点N坐标为(t,n),当m>n时,MN的长度可表示为______;
(2)如图2,四边形OABC的顶点O是坐标原点,点A在第一象限,![]() OAB=90
OAB=90![]() ,OA=AB,点C在第四象限,B点的坐标为(6,0),且OC=5.点P是线段OB上的一个动点(点P不与点0、B重合),过点P作与y轴平行的直线l,设点P横坐标为t.
,OA=AB,点C在第四象限,B点的坐标为(6,0),且OC=5.点P是线段OB上的一个动点(点P不与点0、B重合),过点P作与y轴平行的直线l,设点P横坐标为t.
①已知当t=4时,直线l恰好经过点C,求点A、C两点的坐标;
②在①的条件下,直线l上有一点M,当MB=![]() OC时,直接写出满足条件的点M坐标;
OC时,直接写出满足条件的点M坐标;
③如图3延长线段BA交y轴于点D将线段BD顺时针旋转60![]() ,D点的对应点为点E,是否存 在x轴上的点Q,使得QD+QE的值最小,若存在请求出点Q的坐标,并求出
,D点的对应点为点E,是否存 在x轴上的点Q,使得QD+QE的值最小,若存在请求出点Q的坐标,并求出![]() OQD的度数; 若不存在,请说明理由.
OQD的度数; 若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com