
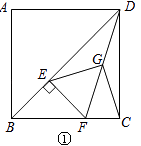
【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG. 
(1)求证:EG=CG;EG⊥CG.
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
【答案】
(1)证明:如图①中,∵四边形ABCD是正方形,
∴∠BCD=∠ADC=90°,∠BDC= ![]() ,
,
∵EF⊥BD,
∴∠DEF=90°,
∵GF=GD,
∴EG=DG=GF= ![]() DF,GC=DG=GF=
DF,GC=DG=GF= ![]() DF,
DF,
∴EG=GC,∠GED=∠GDE,∠GCD=∠GDC,
∵∠EGF=∠GED+∠GDE=2∠EDG,∠CGF=∠GCD+∠GDC=2∠GDC,
∴∠EGC=∠EGF+∠CGF=2∠EDG+2∠GDC=2(∠EDG+∠GDC)=90°,
∴EG⊥GC
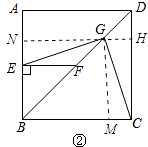
(2)证明:图②中,结论仍然成立.
理由:作GM⊥BC于M,⊥AB于N交CD于H.
∵四边形ABCD是正方形,
∴∠A=∠ADC=90°,∠ABD=∠DBC=∠BDC=45°
∴GM=GN,
∵∠A=∠ANG=∠ADH=90°,
∴四边形ANHD是矩形,
∴∠DHN=90°,∠GDH=∠HGD=45°,
∴HG=DH=AN,同理GH=CM,
∵∠ENG=∠A=∠BEF=90°,
∴EF∥GN∥AD,∵GF=GD,
∴AN=NE=GH=MC,
在△GNE和△GMC中,
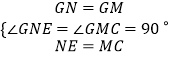 ,
,
∴△GNE≌△GMC,
∴GE=GC,∠NGE=∠MGC,
∴∠EGC=∠NGM=90°,
∴EG⊥GC.
【解析】(1)根据直角三角形斜边中线的性质以及三角形外角定理即可证明.(2)作GM⊥BC于M,⊥AB于N交CD于H,只要证明△GNE≌△GMC即可解决问题.


科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,O为坐标原点,点P是反比例函数y= ![]() (x>0)图象上的一个动点,若以点P为圆心,3为半径的圆与直线y=x相交,交点为A,B,当弦AB的长等于2
(x>0)图象上的一个动点,若以点P为圆心,3为半径的圆与直线y=x相交,交点为A,B,当弦AB的长等于2 ![]() 时,点P的坐标为( )
时,点P的坐标为( ) 
A.(1,6)和(6,1)
B.(2,3)和(3,2)??
C.( ![]() ,3
,3 ![]() )和(3
)和(3 ![]() ,
, ![]() )
)
D.( ![]() ,2
,2 ![]() )和(2
)和(2 ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年《政府工作报告》中提出了十大新词汇,为了解同学们对新词汇的关注度,某数学兴趣小组选取其中的A:“互联网+政务服务”,B:“工匠精神”,C:“光网城市”,D:“大众旅游时代”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词.根据调查结果,该小组绘制了如下的两幅不完整的统计图. 
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了多少名同学?
(2)条形统计图中,m= , n=;
(3)扇形统计图中,热词B所在扇形的圆心角是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG. 
(1)求证:EG=CG;EG⊥CG.
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是平行四边形,对角线OB在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y= ![]() 和y=
和y= ![]() 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
① ![]() =
= ![]() ;
;
②阴影部分面积是 ![]() (k1+k2);
(k1+k2);
③当∠AOC=90°时,|k1|=|k2|;
④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.
其中正确的结论是(把所有正确的结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点D、E分别在△ABC的边AB、AC上,下列给出的条件中,不能判定DE∥BC的是( )
A.BD:AB=CE:AC
B.DE:BC=AB:AD
C.AB:AC=AD:AE
D.AD:DB=AE:EC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,M、N分别是边AB、AC的中点,在射线MN上取点D,使∠ADM=∠BAC,连接AD.
(1)如图1,当BC=3时,求DM的长.
(2)如图2,以AB为底边在AB的左侧作等腰△ABE,并且使顶角∠AEB=2∠BAC,连接EM.
①判断四边形AEMD的形状,并说明理由.
②设BC=x(x>0),四边形AEMD的面积为y,试用含x的式子表示y,并说明是否存在x的值,使得四边形AEMD的面积等于△ABC的面积?若存在,请求出x的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com