
【题目】如图,抛物线与x轴交两点A(﹣1,0),B(3,0),过点A作直线AC与抛物线交于C点,它的坐标为(2,﹣3).
(1)求抛物线及直线AC的解析式;
(2)P是线段AC上的一个动点,(不与A,C重合),过P点作y轴的平行线交抛物线于E点,点E与点A、C围成三角形,求出△ACE面积的最大值;
(3)点G为抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,直接写出所有满足条件的F点坐标;如果不存在,如果不存在,请说明理由.

【答案】(1)直线AC的函数解析式是y=﹣x﹣1;(2)S△ACE=![]() ;(3)存在4个符合条件的F点.
;(3)存在4个符合条件的F点.
【解析】
(1)将A、B坐标代入y=x2+bx+c,利用待定系数法可求得二次函数解析式,设直线AC的解析式为:y=mx+n,将A、C坐标代入,利用待定系数法即可求得直线AC的解析式;
(2)设点P的横坐标为x(﹣1≤x≤2),则P(x,﹣x﹣1),E(x,x2﹣2x﹣3),由S△ACE=![]() PE|xC﹣xA|,而|xC﹣xA|的值是确定的,因此只要求得PE的最大值即可;
PE|xC﹣xA|,而|xC﹣xA|的值是确定的,因此只要求得PE的最大值即可;
(3)分CG与AF平行、CF与AG平行,分别画出符合题意的图形,分别进行求解即可得.
(1)将A(﹣1,0),B(3,0)代入y=x2+bx+c,
得![]() ,解得:
,解得:![]() ,
,
∴y=x2﹣2x﹣3,
设直线AC的解析式为:y=mx+n,
将A、C坐标代入得
![]() ,解得:
,解得:![]() ,
,
∴直线AC的函数解析式是y=﹣x﹣1;
(2)设点P的横坐标为x(﹣1≤x≤2),则P(x,﹣x﹣1),E(x,x2﹣2x﹣3),
∵点P在点E的上方,
∴PE=(﹣x﹣1)﹣(x2﹣2x﹣3)=﹣x2+x+2=﹣(x﹣![]() )2+
)2+![]() ,
,
∴当x=![]() 时,PE的最大值为
时,PE的最大值为![]() ,
,
∴S△ACE=![]() PE|xC﹣xA|=
PE|xC﹣xA|=![]() ×
×![]() ×3=
×3=![]() ;
;
(3)①如图,连接C与抛物线和y轴的交点,
∵C(2,﹣3),G(0,﹣3)
∴CG∥X轴,此时AF=CG=2,
∴F点的坐标是(﹣3,0);
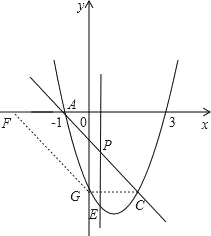
②如图,AF=CG=2,A点的坐标为(﹣1,0),因此F点的坐标为(1,0);
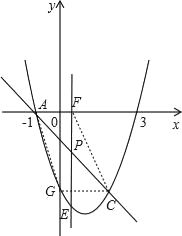
③如图,此时C,G两点的纵坐标互为相反数,因此G点的纵坐标为3,代入抛物线中即可得出G点的坐标为(1±![]() ,3),由于直线GF的斜率与直线AC的相同,因此可设直线GF的解析式为y=﹣x+h,将点代入后可得出直线的解析式为y=﹣x+4+
,3),由于直线GF的斜率与直线AC的相同,因此可设直线GF的解析式为y=﹣x+h,将点代入后可得出直线的解析式为y=﹣x+4+![]() .因此直线GF与x轴的交点F的坐标为(4+
.因此直线GF与x轴的交点F的坐标为(4+![]() ,0);
,0);
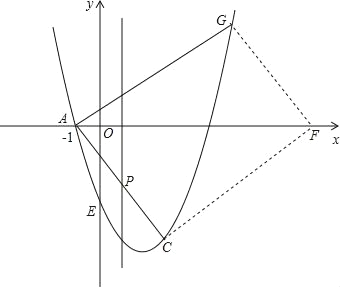
④如图,同③可求出F的坐标为(4﹣![]() ,0);
,0);
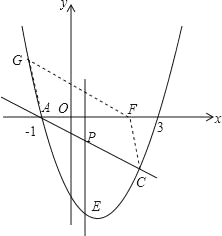
综合四种情况可得出,存在4个这样的点F,分别是F1(1,0),F2(﹣3,0),F3(4+![]() ,0),F4(4﹣
,0),F4(4﹣![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】如图,点M,N分别是正方形ABCD的边BC,CD上的点,且BM=CN, AM与BN交于点P,试探索AM与BN的关系.
(1)数量关系_____________________,并证明;
(2)位置关系_____________________,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=ax+b经过第二、三、四象限,那么下列结论正确的是( )
A. ![]() =a+b
=a+b
B. 点(a,b)在第一象限内
C. 反比例函数![]() ,当x>0时,函数值y随x增大而减小
,当x>0时,函数值y随x增大而减小
D. 抛物线y=ax2+bx+c的对称轴过二、三象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第1次用600元购进2B铅笔若干支,第2次用800元又购进该款铅笔,但这次每支的进价是第1次进价的八折,且购进数量比第1次多了100支.
(1)求第1次每支2B铅笔的进价;
(2)若要求这两次购进的2B铅笔按同一价格全部销售完毕后获利不低于600元,问每支2B铅笔的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我国经济的发展,高铁逐渐成为了主要的交通工具,一般的高铁G字头的高速动车组以D字头的动车组,由大连到北京的G377的平均速度是D31的平均速度的![]() 倍,行驶相同的路程
倍,行驶相同的路程![]() 千米,G377少用
千米,G377少用![]() 个小时。
个小时。
(1)求D31的平均速度。
(2)若以“速度与票价的比值”定义这两种列车的性价比,人们出行都喜欢选择性价比高的方式,现阶段D31票价为![]() 元/张,G377票件为
元/张,G377票件为![]() 元/张,如果你又机会给有关部门提一个合理化建议,使G377得性价比达到D31的性价比,你如何建议,为什么?
元/张,如果你又机会给有关部门提一个合理化建议,使G377得性价比达到D31的性价比,你如何建议,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,射线AP在△ABC的外侧,点B关于AP的对称点为D,连接CD交射线AP于点E,连接BE.
(1)根据题意补全图形;
(2)求证:CD=EB+EC;
(3)求证:∠ABE=∠ACE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是⊙
是⊙![]() 的直径,
的直径,![]() ,
,![]() 和
和![]() 是圆
是圆![]() 的两条切线,
的两条切线,![]() ,
,![]() 为切点,过圆上一点
为切点,过圆上一点![]() 作⊙
作⊙![]() 的切线
的切线![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() ,
,![]() .若
.若![]() ,则
,则![]() 等于( )
等于( )

A. 0.5 B. 1
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为______.
周长的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形
(1) 如图1,点E在线段AB上,点D在射线CB上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF,连接EF,猜想线段AB、DB、AF之间的数量关系
(2) 点E在线段BA的延长线上,其他条件与(1)中的一致,请在图2上将图形补充完整,并猜想证明线段AB、DB、AF之间的数量关系

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com