
 一副量角器与一块含30°锐角的三角板如图所示放置,三角板的顶点C恰好落在量角器的直径MN上,顶点A,B恰好落在量角器的圆弧上,且AB∥MN.若AB=8,则量角器的直径MN=4$\sqrt{7}$.
一副量角器与一块含30°锐角的三角板如图所示放置,三角板的顶点C恰好落在量角器的直径MN上,顶点A,B恰好落在量角器的圆弧上,且AB∥MN.若AB=8,则量角器的直径MN=4$\sqrt{7}$. 分析 作CD⊥AB于点D,取圆心O,连接OA,作OE⊥AB于点E,首先求得CD的长,即OE的长,在直角△AOE中,利用勾股定理求得半径OA的长,则MN即可求解.
解答 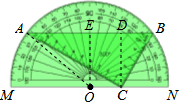 解:作CD⊥AB于点D,取圆心O,连接OA,作OE⊥AB于点E.
解:作CD⊥AB于点D,取圆心O,连接OA,作OE⊥AB于点E.
在直角△ABC中,∠A=30°,则BC=$\frac{1}{2}$AB=4,
在直角△BCD中,∠B=90°-∠A=60°,
∴CD=BC•sinB=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴OE=CD=2$\sqrt{3}$,
在△AOE中,AE=$\frac{1}{2}$AB=4,
则OA=$\sqrt{A{E}^{2}+O{E}^{2}}$=$\sqrt{16+12}$=2$\sqrt{7}$,
则MN=2OA=4$\sqrt{7}$.
故答案是:4$\sqrt{7}$.
点评 本题考查了垂径定理的应用,在半径或直径、弦长以及弦心距之间的计算中,常用的方法是转化为解直角三角形.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠ABC=90°,BD为AC边的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AB=12,BC=5,则四边形BDFG的周长为26.
如图,在△ABC中,∠ABC=90°,BD为AC边的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AB=12,BC=5,则四边形BDFG的周长为26.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,某工厂师傅要在一个面积为15m2的矩形钢板上裁剪下两个相邻的正方形钢板当工作台的桌面,且要使大正方形的边长比小正方形的边长大1m,则裁剪后剩下的阴影部分的面积为2m2.
如图,某工厂师傅要在一个面积为15m2的矩形钢板上裁剪下两个相邻的正方形钢板当工作台的桌面,且要使大正方形的边长比小正方形的边长大1m,则裁剪后剩下的阴影部分的面积为2m2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com