
阅读材料:已知方程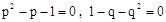 且
且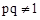 ,求
,求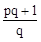 的值.
的值.
解:由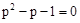 ,及
,及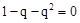 可知
可知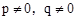 ,又∵
,又∵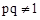 ,∴
,∴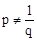 .
.
∵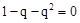 可变形为
可变形为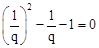 ,根据
,根据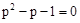 和
和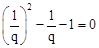 的特征.
的特征.
∴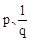 是方程
是方程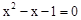 的两个不相等的实数根,则
的两个不相等的实数根,则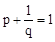 ,即
,即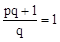 .
.
根据阅读材料所提供的方法,完成下面的解答.
已知: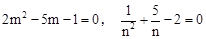 ,且
,且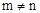 ,求下列各式的值(1)
,求下列各式的值(1)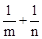 ;(2)
;(2)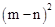 .
.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:阅读理解
| pq+1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| pq+1 |
| q |
| 1 |
| n2 |
| 5 |
| n |
| 1 |
| m |
| 1 |
| n |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| pq+1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| pq+1 |
| q |
| 1 |
| n2 |
| 5 |
| n |
| 1 |
| m |
| 1 |
| n |
查看答案和解析>>
科目:初中数学 来源: 题型:
| b |
| a |
| c |
| a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 的值.
的值. .
. )2-(
)2-( )-1=0,根据p2-p-1=0和(
)-1=0,根据p2-p-1=0和( )2-(
)2-( )-1=0的特征.
)-1=0的特征. 是方程x2-x-1=0的两个不相等的实数根,则p+
是方程x2-x-1=0的两个不相等的实数根,则p+ =1,即
=1,即 =1.
=1. +
+ -2=0且m≠n,求下列各式的值:(1)
-2=0且m≠n,求下列各式的值:(1) +
+ ;(2)(m-n)2.
;(2)(m-n)2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com