
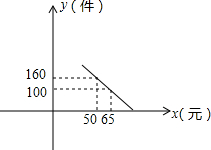
 某校两大学生积极响应“自主创业”的号召,准备利用一个月假期投资销售一种进价为每件40元的小家电,通过试管营销发现,当销售单价在40元至100元之间(含40元和100元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数.其图象如图所示.
某校两大学生积极响应“自主创业”的号召,准备利用一个月假期投资销售一种进价为每件40元的小家电,通过试管营销发现,当销售单价在40元至100元之间(含40元和100元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数.其图象如图所示.分析 (1)待定系数法求解即可得;
(2)根据:总利润=每件小家电利润×销售量,可得总利润W关于x的函数关系式,根据二次函数性质可得总利润的最大值,比较后可得答案.
解答 解:(1)设y与x的函数关系式为:y=kx+b(k≠0),
由题意得,$\left\{\begin{array}{l}{50k+b=160}\\{65k+b=100}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-4}\\{b=360}\end{array}\right.$.
故y与x的函数表达式为y=-4x+360(40≤x≤100).
(2)设销售该小家电获取的总利润为W,
则W=(x-40)(-4x+360)
=-4x2+520x-14400
=-4(x-65)2+2500,
∵-4<0,
∴当x=65时,W取得最大值,W最大值=2500,
∵$\frac{2500}{2}$<1300,1300-$\frac{2500}{2}$=50,
∴他们的想法不能实现,每人与预期相比差50元.
点评 本题主要考查待定系数法求函数解析式及二次函数的实际应用,理解题意抓住相等关系并列出函数解析式是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
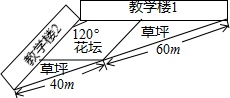 学校两幢教学楼之间有一块三角形地带,将其划分为三个区域:一块菱形和两块三角形.菱形作为花坛,两个三角形内铺上草皮,两幢教学楼的夹角为120°,其余尺寸如图所示,则菱形花坛的面积为$\frac{7200\sqrt{3}}{19}$m2.
学校两幢教学楼之间有一块三角形地带,将其划分为三个区域:一块菱形和两块三角形.菱形作为花坛,两个三角形内铺上草皮,两幢教学楼的夹角为120°,其余尺寸如图所示,则菱形花坛的面积为$\frac{7200\sqrt{3}}{19}$m2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com