
【题目】如图,四边形ABCD中,AB=CB,AD=CD,对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E、F.求证:OE=OF.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
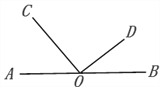
【题目】如图,O是直线AB上的一点,OC⊥OD,垂足为O.
(1)若∠BOD=32°,求∠AOC的度数;
(2)若∠AOC:∠BOD=2:1,直接写出∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016广东省深圳市第23题)如图,抛物线![]() 与
与![]() 轴交于A、B两点,且B(1 , 0)。
轴交于A、B两点,且B(1 , 0)。
(1)、求抛物线的解析式和点A的坐标;
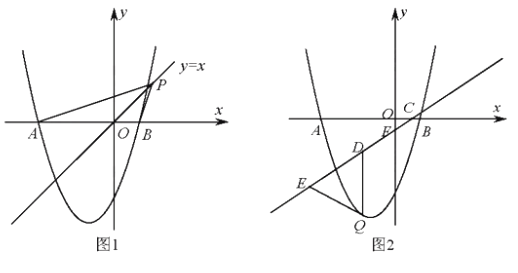
(2)、如图1,点P是直线![]() 上的动点,当直线
上的动点,当直线![]() 平分∠APB时,求点P的坐标;
平分∠APB时,求点P的坐标;
(3)如图2,已知直线![]() 分别与
分别与![]() 轴
轴 ![]() 轴 交于C、F两点。点Q是直线CF下方的抛物线上的一个动点,过点Q作
轴 交于C、F两点。点Q是直线CF下方的抛物线上的一个动点,过点Q作 ![]() 轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE。问以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由。
轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE。问以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
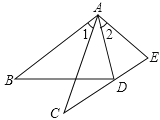
【题目】在数学课上,林老师在黑板上画出如图所示的△ABD和△ACE两个三角形,并写出四个条件:①AB=AC;②AD=AE;③∠1=∠2;④∠B=∠C.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
题设:___________;结论:_______.(均填写序号)
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016四川省乐山市第26题)如图1,二次函数![]() 的图象与
的图象与![]() 轴分别交于A、B两点,与
轴分别交于A、B两点,与![]() 轴交于点C.若tan∠ABC=3,一元二次方程
轴交于点C.若tan∠ABC=3,一元二次方程![]() 的两根为-8、2.
的两根为-8、2.
(1)求二次函数的解析式;
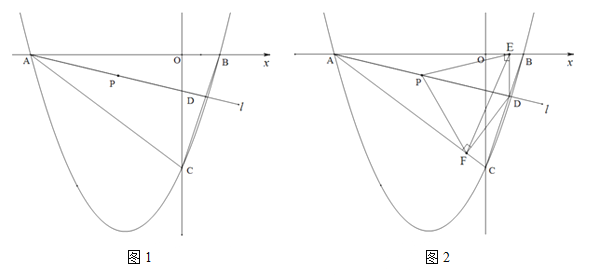
(2)直线![]() 绕点A以AB为起始位置顺时针旋转到AC位置停止,
绕点A以AB为起始位置顺时针旋转到AC位置停止,![]() 与线段BC交于点D,P是AD的中点.
与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
②如图2,过点D作DE垂直![]() 轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在
轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在![]() 运动过程中,∠EPF的大小是否改变?请说明理由;
运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结![]() ,求△PEF周长的最小值.
,求△PEF周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个面积为150平方米的长方形养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙,墙长为18米,另三边用篱笆围成,如篱笆长度为35米,且要求用完。求鸡场的长与宽各是多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com