练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．运用乘法公式计算
    （1）（3x-5）2-（2x+7）2；
    （2）（x-y+1）（x+y-1）；
    （3）（2x-y-3）2；
    （4）（x+2）2（x-2）2；
    （5）（a+2）（a-2）（a2+4）（a4+16）；
    （6）（a+2b+3c）2．

    分析 根据平方差公式即可化简运算．

    解答 解：（1）原式=（3x-5-2x-7）（3x-5+2x+7）=5x2-58x-24；
    （2）原式=[x-（y-1）][x+（y-1）]=x2-（y-1）2=x2-y2+2y-1；
    （3）原式=[（2x-y）-3]2=（2x-y）2-6（2x-y）+9=4x2-4xy+y2-12x+6y+9
    （4）原式=[（x+2）（x-2）]2=（x2-4）2=x4-8x2+14
    （5）原式=（a2-4）（a2+4）（a4+16）=（a4-16）（a4+16）=a8-256
    （6）原式=[（a+2b）+3c]2=（a+2b）2+6c（a+2b）+9c2=a2+4ab+4b2+6ac+12ab+9c2

    点评 本题考查整式运算，涉及平方差公式，完全平方公式，还注意利用整体的思想进行运算．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．已知$\frac{a}{b}$=$\frac{b}{c}$=$\frac{c}{a}$，求$\frac{a+b-c}{a-b+c}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

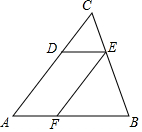    11．如图，点D、E、F分别是△ABC的边AC、BC、AB上的点，且有$\frac{CE}{CB}$=$\frac{CD}{CA}$=$\frac{1}{3}$，$\frac{BF}{BA}$=$\frac{BE}{BC}$=$\frac{2}{3}$，当△ABC的面积为18cm2时，求四边形AFED的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

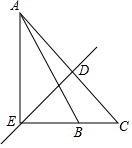    8．如图，在△ABC中，作AC的垂直平分线，交AC于点D，交CB的延长线于点E，连接AE，且AE⊥EC．已知AE比BE长3，S△ABC=12，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

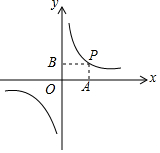    15．反比例函数y=$\frac{8}{x}$的图象如图所示，在第一象限的图象上任取一点P（x，y），作PA⊥x轴于点A，PB⊥y轴于点B．
    （1）请填写入表：
     x … $\frac{1}{2}$ 1 23  4 5 …
     y  …        …
     S四边形OAPB  …        …
    （2）由（1）的结果，你能得出怎样的结论？
    （3）若点P位于反比例函数y=$\frac{8}{x}$图象在第三象限的一支上，则（2）的结论还成立吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．某地电话拨号上网有两种收费方式：用户可任取其一：计时制：0.05元/分钟；包月制：50元/月（只限一部宅电上网）．此外每种上网方式都加收通信费0.02元/分钟．
    （1）一个月内上网15小时和20小时，按两种收费方式各需多少元？
    （2）一个月内上网t小时，会出现两种计费方式的收费一样的情况吗？
    （3）某用户一个月内估计上网18小时，你认为采用哪种方式合算？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知抛物线y=5x2+（m2-4）x+1-m的顶点在y轴的正半轴上，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．若单项式-m2n3x+5与m2n4x+3的和还是单项式，试求x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知：如图，将矩形ABCD绕点B按顺时针方向旋转一个角α（0°＜α＜180°），得矩形BEFG，直线BG，EF交直线CD于点P，H．找出与BP相等的线段，并给出证明．

    查看答案和解析>>

    同步练习册答案