Question

如图，在梯形ABCD中，AD∥BC，AD=2，BC=4，点M是AD的中点，△MBC是等边三角形．

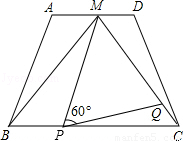
（1）求证：梯形ABCD是等腰梯形；

（2）动点P、Q分别在线段BC和MC上运动，且∠MPQ=60°保持不变．设PC=x，MQ=y，求y与x的函数关系式；

（3）在（2）中：

①当动点P、Q运动到何处时，以点P、M和点A、B、C、D中的两个点为顶点的四边形是平行四边形？并指出符合条件的平行四边形的个数；

②当y取最小值时，判断△PQC的形状，并说明理由．

 

Answer 1

【答案】

(1)见解析；（2）y=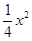﹣x+4．

（2）①当BP=1，MQ=或BP=3，符合条件的平行四边形的个数有4个．②△PQC是直角三角形．

【解析】

试题分析：（1）要证梯形ABCD是等腰梯形，只需证△AMB≌△DMC．

（2）由△BMP∽△CQP，可得到BP与CQ的关系，从而转化成y与x的函数关系式．

（3）先利用二次函数求最值，求出y取最小值时x的值和y的最小值，从而确定P、Q的位置，判断出△PQC的形状．

试题解析：

（1）证明：∵△MBC是等边三角形，

∴MB=MC，∠MBC=∠MCB=60°．

∵M是AD中点，

∴AM=MD．

∵AD∥BC，

∴∠AMB=∠MBC=60°，∠DMC=∠MCB=60°．

∴△AMB≌△DMC．

∴AB=DC．

∴梯形ABCD是等腰梯形．

（2）在等边△MBC中，MB=MC=BC=4，∠MBC=∠MCB=60°，∠MPQ=60°，

∴∠BMP+∠BPM=∠BPM+∠QPC=120°．

∴∠BMP=∠QPC．

∴△BPM∽△CQP．

∴．

∵PC=x，MQ=y，

∴BP=4﹣x，QC=4﹣y．

∴．

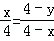∴y=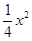﹣x+4．（8分）

（3）①当BP=1时，则有BPAM，BPMD，

则四边形ABPM为平行四边形，

∴MQ=y=×3²﹣3+4=．（8分）

当BP=3时，则有PCAM，PCMD，

则四边形MPCD为平行四边形，

∴MQ=y=×1²﹣1+4=．（9分）

∴当BP=1，MQ=或BP=3，MQ=时，

以P、M和A、B、C、D中的两个点为顶点的四边形是平行四边形．此时平行四边形有2个．

故符合条件的平行四边形的个数有4个．

②△PQC为直角三角形．

∵y=（x﹣2）²+3，

∴当y取最小值时，x=PC=2．

∴P是BC的中点，MP⊥BC，而∠MPQ=60°，

∴∠CPQ=30°，

∴∠PQC=90°．

∴△PQC是直角三角形．

考点：1.等腰梯形的判定；2.二次函数的最值；3.等边三角形的性质．