
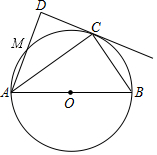
 如图,⊙O的直径AB长为12,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.
如图,⊙O的直径AB长为12,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.分析 (1)连接OC,根据切线性质求出OC⊥CD,根据平行线的判定得出AD∥OC,即可求出答案;
(2)连接BM和OM,求出∠AOM的度数,根据弧长公式求出即可.
解答 (1)证明:连接OC,
∵DC是⊙O的切线,
∴OC⊥DC,
∵AD⊥CD,
∴AD∥OC,
∴∠DAC=∠OCA,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠DAC=∠OAC,
即AC平分∠DAB;
(2)解:
连接BM、OM,
∵AB是⊙O的直径,
∴∠AMB=90°,∠ACB=90°,
∵∠ABC=60°,
∴∠CAB=30°,
∴∠DAB=2×30°=60°,
∴∠MBA=30°,
∴∠MOA=60°,
∴弧AM的长为:$\frac{12π×60}{360}$=2π.
点评 本题考查了切线的性质和弧长公式等知识点,能灵活运用定理进行推理和计算是解此题的关键.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:填空题
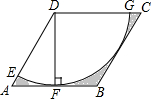 如图,在菱形ABCD中,∠DAB=60°,AD=6,DF⊥AB,以点D为圆心,DF为半径作圆弧,分别交AD,CD于点E,G,则图中阴影部分的面积为18$\sqrt{3}$-9π(结果保留π)
如图,在菱形ABCD中,∠DAB=60°,AD=6,DF⊥AB,以点D为圆心,DF为半径作圆弧,分别交AD,CD于点E,G,则图中阴影部分的面积为18$\sqrt{3}$-9π(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.35×1010元 | B. | 3.5×108元 | C. | 3.5×109元 | D. | 35×108元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
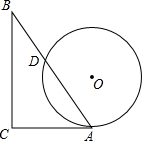 如图,一个含有30°角的直角三角板ABC的直角边AC与⊙O相切于点A,∠C=90°,∠B=30°,⊙O的直径为4,AB与⊙O相交于D点,则AD的长为2$\sqrt{3}$.
如图,一个含有30°角的直角三角板ABC的直角边AC与⊙O相切于点A,∠C=90°,∠B=30°,⊙O的直径为4,AB与⊙O相交于D点,则AD的长为2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com