
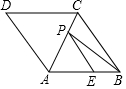
 如图,菱形ABCD的边长为5,对角线AC=2$\sqrt{5}$,点E在边AB上,BE=2,点P是AC上的一个动点,则PB+PE的最小值为2$\sqrt{13}$.
如图,菱形ABCD的边长为5,对角线AC=2$\sqrt{5}$,点E在边AB上,BE=2,点P是AC上的一个动点,则PB+PE的最小值为2$\sqrt{13}$. 分析 找出B点关于AC的对称点D,连接DE交AC于P,则DE就是PB+PE的最小值,求出即可.
解答 解:∵点B,D关于直线AC对称,
∴连接DE交AC于一点P,
则DE=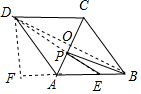 PB+PE的最小值,
PB+PE的最小值,
连接BD,
∵四边形ABCD是菱形,
∴BD⊥AC,AO=$\frac{1}{2}$AC=$\sqrt{5}$,
∴DO=2$\sqrt{5}$,
∴BD=4$\sqrt{5}$,
过D作DF⊥AB交BA的延长线于F,
∴AB•DF=$\frac{1}{2}$AC•BD,
∴DF=4,
∴AF=3
∴EF=6,
∴DE=$\sqrt{D{F}^{2}+E{F}^{2}}$=2$\sqrt{13}$.
∴PB+PE的最小值为2$\sqrt{13}$.
故答案为:2$\sqrt{13}$.
点评 本题主要考查轴对称-最短路线问题,菱形的性质,勾股定理等知识点,确定P点的位置是解答本题的关键.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 119×104 | B. | 11.9×105 | C. | 1.19×106 | D. | 0.119×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 阅读材料
阅读材料查看答案和解析>>
科目:初中数学 来源: 题型:解答题
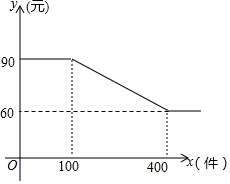 某衬衫厂生产某品牌衬衫的成本价为50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍.
某衬衫厂生产某品牌衬衫的成本价为50元/件,批发价y元/件与一次性批发件数x件之间的关系满足图中折线的函数关系,批发件数为10的正整数倍.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com