
 花圃.设花圃的边AB长为x,花圃的面积为s米2.
花圃.设花圃的边AB长为x,花圃的面积为s米2.| b |
| 2a |
| 4ac-b2 |
| 4a |
科目:初中数学 来源: 题型:解答题
 花圃.设花圃的边AB长为x,花圃的面积为s米2.
花圃.设花圃的边AB长为x,花圃的面积为s米2. 时,
时,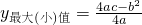 )
)查看答案和解析>>
科目:初中数学 来源: 题型:
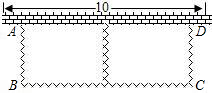
如图所示,有长24米的篱笆,一面利用墙(墙的最大长度为10米),围成中间隔有一道篱笆的长方形花圃.设花圃的边AB长为x,花圃的面积为s米2.
(1)请求出s与x的函数关系式.
(2)所围的花圃面积能否是48米2 ? 若能,求出的x值; 若不能,请说明理由.
(参考公式:二次函数y=ax2+bx+c,当x=-![]() 时,
时,![]() )
)
 |
查看答案和解析>>
科目:初中数学 来源:2008-2009学年黑龙江省哈尔滨市第69中学九年级(上)期中数学试卷(解析版) 题型:解答题
 时,
时, )
)
查看答案和解析>>
科目:初中数学 来源:2012年10月中考数学模拟试卷(20)(解析版) 题型:解答题
 时,
时, )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com