
ΓΨΧβΡΩΓΩ÷ΤΉς“Μ÷÷≤ζΤΖΘ§–ηœ»ΫΪ≤ΡΝœΦ”»»¥οΒΫ60 ΓφΚσΘ§‘ΌΫχ––≤ΌΉςΘ°…ηΗΟ≤ΡΝœΈ¬Ε»ΈΣyΘ®ΓφΘ©Θ§¥”Φ”»»ΩΣ ΦΦΤΥψΒΡ ±ΦδΈΣxΘ®minΘ©Θ°ΨίΝΥΫβΘ§Β±ΗΟ≤ΡΝœΦ”»» ±Θ§Έ¬Ε»y”κ ±Φδx≥…“Μ¥ΈΚ· ΐΙΊœΒΘΜΆΘ÷ΙΦ”»»Ϋχ––≤ΌΉς ±Θ§Έ¬Ε»y”κ ±Φδx≥…Ζ¥±»άΐΙΊœΒΘ®»γΆΦΘ©Θ°“―÷ΣΗΟ≤ΡΝœ‘Ύ≤ΌΉςΦ”»»«ΑΒΡΈ¬Ε»ΈΣ15 ΓφΘ§Φ”»»5Ζ÷÷”ΚσΈ¬Ε»¥οΒΫ60 ΓφΘ°
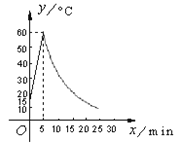
Θ®1Θ©Ζ÷±π«σ≥ωΫΪ≤ΡΝœΦ”»»ΚΆΆΘ÷ΙΦ”»»Ϋχ––≤ΌΉς ±Θ§y”κxΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®2Θ©ΗυΨίΙΛ“’“Σ«σΘ§Β±≤ΡΝœΒΡΈ¬Ε»ΒΆ”Ύ15 Γφ ±Θ§–κΆΘ÷Ι≤ΌΉςΘ§Ρ«Ο¥¥”ΩΣ ΦΦ”»»ΒΫΆΘ÷Ι≤ΌΉςΘ§Ι≤Ψ≠άζΝΥΕύ…Ό ±ΦδΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©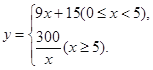 Θ®2Θ©20Ζ÷÷”
Θ®2Θ©20Ζ÷÷”
ΓΨΫβΈωΓΩΫβΘΚΘ®1Θ©≤ΡΝœΦ”»» ±Θ§…ηy=ax+15Θ®aΓΌ0Θ©Θ§
”…Χβ“βΒΟ60=5a+15Θ§
ΫβΒΟa=9Θ§
‘ρ≤ΡΝœΦ”»» ±Θ§y”κxΒΡΚ· ΐΙΊœΒ ΫΈΣy=9x+15Θ®0ΓήxΓή5Θ©Θ°
ΆΘ÷ΙΦ”»» ±Θ§…ηy=Θ®kΓΌ0Θ©Θ§
”…Χβ“βΒΟ60=Θ§
ΫβΒΟk=300Θ§
‘ρΆΘ÷ΙΦ”»»Ϋχ––≤ΌΉς ±y”κxΒΡΚ· ΐΙΊœΒ ΫΈΣy=![]() Θ®xΓί5Θ©ΘΜ
Θ®xΓί5Θ©ΘΜ
Θ®2Θ©Α―y=15¥ζ»κy=![]() Θ§ΒΟx=20Θ§
Θ§ΒΟx=20Θ§
“ρ¥Υ¥”ΩΣ ΦΦ”»»ΒΫΆΘ÷Ι≤ΌΉςΘ§Ι≤Ψ≠άζΝΥ20Ζ÷÷”Θ°
¥πΘΚ¥”ΩΣ ΦΦ”»»ΒΫΆΘ÷Ι≤ΌΉςΘ§Ι≤Ψ≠άζΝΥ20Ζ÷÷”Θ°


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
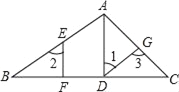
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ADΓΆBCΘ§¥ΙΉψΈΣDΘ§ΒψE‘ΎAB…œΘ§EFΓΆBCΘ§¥ΙΉψΈΣFΘ°
(1)AD”κEFΤΫ––¬πΘΩΈΣ ≤Ο¥ΘΩ
(2)»γΙϊΓœ1ΘΫΓœ2Θ§«“Γœ3ΘΫ115ΓψΘ§«σΓœBACΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΓςABCΡΎΫ””ΎΓ―PΘ§AB «Γ―PΒΡ÷±ΨΕΘ§AΘ®©¹1Θ§0Θ©CΘ®3Θ§2 ![]() Θ©Θ§BCΒΡ―”≥ΛœΏΫΜy÷α”ΎΒψDΘ§ΒψF «y÷α…œΒΡ“ΜΕ·ΒψΘ§Ν§Ϋ”FC≤Δ―”≥ΛΫΜx÷α”ΎΒψEΘ°
Θ©Θ§BCΒΡ―”≥ΛœΏΫΜy÷α”ΎΒψDΘ§ΒψF «y÷α…œΒΡ“ΜΕ·ΒψΘ§Ν§Ϋ”FC≤Δ―”≥ΛΫΜx÷α”ΎΒψEΘ° 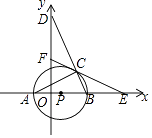
Θ®1Θ©«σΓ―PΒΡΑκΨΕΘΜ
Θ®2Θ©Β±ΓœA=ΓœDCF ±Θ§«σ÷ΛΘΚCE «Γ―PΒΡ«–œΏΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®7Ζ÷Θ©»γΆΦΘ§’ΐ±»άΐΚ· ΐ![]() ΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐ
ΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐ![]()
![]() ‘ΎΒΎ“Μœσœό
‘ΎΒΎ“Μœσœό
ΒΡΆΦœσΫΜ”Ύ![]() ΒψΘ§Ιΐ
ΒψΘ§Ιΐ![]() ΒψΉς
ΒψΉς![]() ÷αΒΡ¥ΙœΏΘ§¥ΙΉψΈΣ
÷αΒΡ¥ΙœΏΘ§¥ΙΉψΈΣ![]() Θ§“―÷Σ
Θ§“―÷Σ![]() ΒΡΟφΜΐΈΣ1.
ΒΡΟφΜΐΈΣ1.
Θ®1Θ©«σΖ¥±»άΐΚ· ΐΒΡΫβΈω ΫΘΜ
Θ®2Θ©»γΙϊ![]() ΈΣΖ¥±»άΐΚ· ΐ‘ΎΒΎ“ΜœσœόΆΦœσ…œΒΡΒψΘ®Βψ
ΈΣΖ¥±»άΐΚ· ΐ‘ΎΒΎ“ΜœσœόΆΦœσ…œΒΡΒψΘ®Βψ![]() ”κΒψ
”κΒψ![]() ≤Μ÷ΊΚœΘ©Θ§«“
≤Μ÷ΊΚœΘ©Θ§«“![]() ΒψΒΡΚαΉχ±ξΈΣ1Θ§‘Ύ
ΒψΒΡΚαΉχ±ξΈΣ1Θ§‘Ύ![]() ÷α…œ«σ“ΜΒψ
÷α…œ«σ“ΜΒψ![]() Θ§ Ι
Θ§ Ι![]() Ήν–Γ.
Ήν–Γ.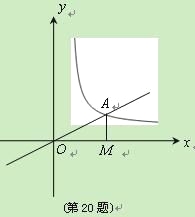
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ Β―ι÷–―ßœ÷”–―ß…ζ2870»ΥΘ§―ß–ΘΈΣΝΥΫχ“Μ≤ΫΖαΗΜ―ß…ζΩΈ”ύ…ζΜνΘ§ΡβΒς≤ιΗς–Υ»Λ–ΓΉιΜνΕ·«ιΩωΘ§ΈΣ¥Υ–Θ―ß…ζΜαΈ·Ά––Γ»ίΓΔ–Γ“ΉΫχ––“Μ¥ΈΥφΜζ≥ι―υΒς≤ιΘ°ΗυΨί≤…Φ·ΒΫΒΡ ΐΨίΘ§–Γ»ίΜφ÷ΤΒΡΆ≥ΦΤΆΦ1Θ§–Γ“ΉΜφ÷ΤΒΡΆ≥ΦΤΆΦ2Θ®≤ΜΆξ’ϊΘ©»γœ¬ΘΚ «κΡψΗυΨίΆ≥ΦΤΆΦ1ΓΔ2÷–ΧαΙ©ΒΡ–≈œΔΘ§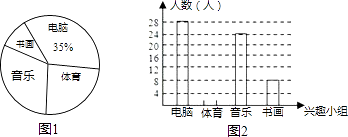
Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©–¥≥ω2Χθ”–Φέ÷Β–≈œΔΘ®≤ΜΑϋά®œ¬Οφ“ΣΦΤΥψΒΡ–≈œΔΘ©ΘΜ
Θ®2Θ©’β¥Έ≥ι―υΒς≤ιΒΡ―υ±Ψ»ίΝΩ «Εύ…ΌΘΩ‘ΎΆΦ2÷–Θ§«κΫΪ–Γ“ΉΜ≠ΒΡΆ≥ΦΤΆΦ÷–ΒΡΓΑΧε”ΐΓ±≤ΩΖ÷ΒΡΆΦ–Έ≤Ι≥δΆξ’ϊΘΜ
Θ®3Θ©Α°ΚΟΓΑ ιΜ≠Γ±ΒΡ»Υ ΐ’Φ±ΜΒς≤ι»Υ ΐΒΡΑΌΖ÷ ΐ «Εύ…ΌΘΩΙάΦΤ Β―ι÷–―ßœ÷”–ΒΡ―ß…ζ÷–Θ§”–Εύ…Ό»ΥΑ°ΚΟΓΑ ιΜ≠Γ±ΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
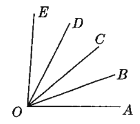
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΓœAOB=20ΓψΘ§ΓœAOE=86ΓψΘ§OBΤΫΖ÷ΓœAOCΘ§ODΤΫΖ÷ΓœCOE.
(1)ΓœCODΒΡΕ» ΐ «______ΘΜ
(2)»τ“‘OΈΣΙέ≤λ÷––ΡΘ§OAΈΣ’ΐΕΪΖΫœρΘ§…δœΏOD‘Ύ ≤Ο¥ΈΜ÷ΟΘΩ
(3)»τ“‘OAΈΣ÷”Οφ…œΒΡ ±’κΘ§ODΈΣΖ÷’κΘ§«“OA’ΐΚΟ‘ΎΓΑ ±ΩΧ3Γ±ΒΡœ¬ΖΫ≤Μ‘ΕΘ§«σ≥ω¥Υ ±ΒΡ ±ΩΧ.(ΫαΙϊΨΪ»ΖΒΫΖ÷÷”)
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–ΈABCD÷–Θ§AB=4Θ§ΒψEΘ§FΖ÷±π‘ΎBCΘ§CD…œΘ§ΫΪΓςABE―ΊAE’έΒΰΘ§ ΙΒψB¬δ‘ΎAC…œΒΡΒψBΓδ¥ΠΘ§”÷ΫΪΓςCEF―ΊEF’έΒΰΘ§ ΙΒψC¬δ‘Ύ÷±œΏEBΓδ”κADΒΡΫΜΒψCΓδ¥ΠΘ§DF= Θ° 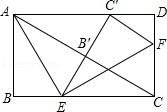
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
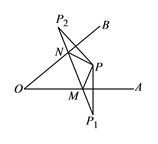
ΓΨΧβΡΩΓΩ»γΆΦΥυ Ψ,ΓœA0B=420Θ§ΒψPΈΣΓœA0BΡΎ“ΜΒψΘ§Ζ÷±πΉς≥ωPΒψΙΊ”ΎOAΓΔOBΒΡΕ‘≥ΤΒψP1Θ§P2Θ§Ν§Ϋ”P1P2ΫΜOA”ΎMΘ§ΫΜOB”ΎNΘ§P1P2=15Θ§‘ρΓςPMNΒΡ÷ή≥ΛΈΣ________Θ§ΓœMPN ________.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΫ≠Ρœ≈©≥Γ ’Ην–Γ¬σΘ§“―÷Σ1Χ®¥σ–Ά ’ΗνΜζΚΆ3Χ®–Γ–Ά ’ΗνΜζ1–Γ ±Ω…“‘ ’Ην–Γ¬σ1.4ΙΪ«ξΘ§2Χ®¥σ–Ά ’ΗνΜζΚΆ5Χ®–Γ–Ά ’ΗνΜζ1–Γ ±Ω…“‘ ’Ην–Γ¬σ2.5ΙΪ«ξΘ°
Θ®1Θ©ΟΩΧ®¥σ–Ά ’ΗνΜζΚΆΟΩΧ®–Γ–Ά ’ΗνΜζ1–Γ ± ’Ην–Γ¬σΗςΕύ…ΌΙΪ«ξΘΩ
Θ®2Θ©¥σ–Ά ’ΗνΜζΟΩ–Γ ±Ζ―”ΟΈΣ300‘ΣΘ§–Γ–Ά ’ΗνΜζΟΩ–Γ ±Ζ―”ΟΈΣ200‘ΣΘ§ΝΫ÷÷–ΆΚ≈ΒΡ ’ΗνΜζ“ΜΙ≤”–10Χ®Θ§“Σ«σ2–Γ ±Άξ≥…8ΙΪ«ξ–Γ¬σΒΡ ’Ην»ΈΈώΘ§«“ΉήΖ―”Ο≤Μ≥§Ιΐ5400‘ΣΘ§”–ΦΗ÷÷ΖΫΑΗΘΩ«κ÷Η≥ωΖ―”ΟΉνΒΆΒΡ“Μ÷÷ΖΫΑΗΘ§≤Δ«σ≥ωœύ”ΠΒΡΖ―”ΟΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com